题目内容
16．
如图，三棱柱ABC-A1B1C1的各棱长均为2，且侧棱与底面垂直，其正（主）视图如图所示，则此三棱柱侧（左）视图的面积为（ ）| A． | $\sqrt{3}$ | B． | 2$\sqrt{2}$ | C． | 2$\sqrt{3}$ | D． | 4 |
分析 由三视图和题意可知三棱柱是正三棱柱，结合正视图，俯视图，不难得到侧视图，然后求出面积．
解答 解：由三视图和题意可知三棱柱是正三棱柱，底面边长为2，侧棱长2，
结合正视图，俯视图，得到侧视图是矩形，长为2，宽为$\sqrt{3}$，
面积为：2×$\sqrt{3}$=2$\sqrt{3}$．
故选：C．
点评 本题考查由三视图求侧视图的面积，是基础题．
练习册系列答案
相关题目
11．已知函数f（x）=$\left\{\begin{array}{l}{3x+3（x≤-1）}\\{f（x-1）+1（x＞-1）}\end{array}\right.$，方程f（x）=x+1的解从小到大排成一个数列{an}，该数列的前n项和为Sn，则$\frac{2{S}_{n+3}+10}{n}$的最小值为（ ）
| A． | $\frac{28}{3}$ | B． | $\frac{19}{2}$ | C． | 6 | D． | 2$\sqrt{10}$+3 |
1．若实数x，y满足约束条件$\left\{{\begin{array}{l}{x-4y+4≤0}\\{x+y≤1}\\{x≥-3}\end{array}}\right.$，则x-y的最大值是（ ）
| A． | -7 | B． | $-\frac{13}{4}$ | C． | -1 | D． | 7 |
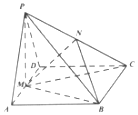已知四棱锥P-ABCD的底面ABCD是菱形，∠ADC=120°，AD的中点M是顶点P的底面ABCD的射影，N是PC的中点．
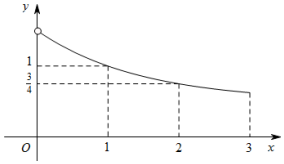已知函数f（x）是定义在[-3，0）∪（0，3]上的奇函数，当x∈（0，3]时，f（x）的图象如图所示，那么满足不等式f（x）≥2x-1 的x的取值范围是[-3，-2]∪[0，1]．
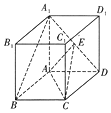如图，在底面是菱形的四棱柱ABCD-A1B1C1D1中，∠ABC=60°，AA1=AC=2，A1B=A1D=2$\sqrt{2}$，点E在A1D上，且E为A1D的中点