题目内容
6.已知命题p:关于x的不等式x3-3x2-9x+2≥m对任意x∈[-2,2]恒成立;命题q:函数y=$\frac{|{x}^{2}-1|}{x-1}$的图象与函数y=mx-2的图象恰有两个交点;若p∨q为真,则实数m的取值范围是(-∞,-20]∪(0,4).分析 命题p:关于x的不等式x3-3x2-9x+2≥m对任意x∈[-2,2]恒成立,?m≤(x3-3x2-9x+2)min,x∈[-2,2].令f(x)=x3-3x2-9x+2,利用导数研究函数的单调性极值与最值即可得出.
命题q:函数y=$\frac{|{x}^{2}-1|}{x-1}$=$\left\{\begin{array}{l}{x+1,x>1或x≤-1}\\{-x-1,-1<x<1}\end{array}\right.$,根据上述函数的图象与函数y=mx-2的图象恰有两个交点,画出图象即可得出m的取值范围.根据p∨q为真,可得p与q必然一真一假.即可得出m的取值范围.
解答 解:命题p:关于x的不等式x3-3x2-9x+2≥m对任意x∈[-2,2]恒成立,
?m≤(x3-3x2-9x+2)min,x∈[-2,2].
令f(x)=x3-3x2-9x+2,则f′(x)=3x2-6x-9=3(x-3)(x+1).
可得:x∈[-2,-1)时,f′(x)>0,此时函数f(x)单调递增;
x∈(-1,2]时,f′(x)<0,此时函数f(x)单调递减.
又f(-2)=0,f(2)=-20,可得x=2时,函数f(x)取得最小值,∴m≤-20.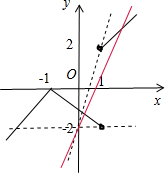
命题q:函数y=$\frac{|{x}^{2}-1|}{x-1}$=$\left\{\begin{array}{l}{x+1,x>1或x≤-1}\\{-x-1,-1<x<1}\end{array}\right.$,
根据上述函数的图象
与函数y=mx-2的图象恰有两个交点,则0<m<4.
若p∨q为真,则p与q必然一真一假.
∴$\left\{\begin{array}{l}{m≤-20}\\{m≤0或m≥4}\end{array}\right.$,或$\left\{\begin{array}{l}{m>-20}\\{0<m<4}\end{array}\right.$,
解得m≤-20,或0<m<4.
实数m的取值范围是m≤-20,或0<m<4.
故答案为:(-∞,-20]∪(0,4).
点评 本题考查了利用导数研究函数的单调性极值与最值、函数图象的交点、简易逻辑的判定方法、数形结合方法,考查了推理能力与计算能力,属于难题.

| A. | 72 | B. | 120 | C. | 192 | D. | 240 |
| A. | 3 | B. | -3 | C. | -$\sqrt{3}$ | D. | $\sqrt{3}$ |
(1)试问:从高一年级学生中随机抽取1人,抽到男生的概率约为多少?
(2)根据抽取的180名学生的调查结果,完成下列列联表.并判断能否在犯错误的概率不超过0.025的前提下认为科类的选择与性别有关?
| 选择自然科学类 | 选择社会科学类 | 合计 | |
| 男生 | 60 | 45 | 105 |
| 女生 | 30 | 45 | 75 |
| 合计 | 90 | 90 | 180 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | $\frac{1}{2}$ | B. | $\frac{3}{5}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 0 |
 如图,三棱柱ABC-A1B1C1的各棱长均为2,且侧棱与底面垂直,其正(主)视图如图所示,则此三棱柱侧(左)视图的面积为( )
如图,三棱柱ABC-A1B1C1的各棱长均为2,且侧棱与底面垂直,其正(主)视图如图所示,则此三棱柱侧(左)视图的面积为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 4 |