题目内容
1.在一次对昼夜温差大小与种子发芽数之间的研究中,研究人员获得了一组样本数据:| 温差x(℃) | 13 | 12 | 11 | 10 | 8 |
| 发芽数y(颗) | 30 | 26 | 25 | 23 | 16 |
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归直线方程是可靠的,请问(1)中所得的线性回归方程是否可靠?
分析 (1)根据表中数据,计算$\overline{x}$、$\overline{y}$,求出回归系数,写出线性回归方程;
(2)利用回归方程计算x=10和x=8时$\stackrel{∧}{y}$的值,验证所得到的线性回归直线方程是可靠的.
解答 解:(1)由表中前3组数据,
计算$\overline{x}$=$\frac{1}{3}$×(13+12+11)=12,
$\overline{y}$=$\frac{1}{3}$×(30+26+25)=27,
且3$\overline{x}$$\overline{y}$=972,
${{\sum_{i=1}^{3}x}_{i}y}_{i}$=977,$\sum_{i=1}^{3}$${{x}_{i}}^{2}$=434,3${\overline{x}}^{2}$=432,
∴$\stackrel{∧}{b}$=$\frac{977-972}{434-432}$=$\frac{5}{2}$,
$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$=27-$\frac{5}{2}$×12=-3;
∴y关于x的线性回归方程是$\stackrel{∧}{y}$=$\frac{5}{2}$x-3;
(2)当x=10时,$\stackrel{∧}{y}$=$\frac{5}{2}$×10-3=22,
则|22-23|<2;
当x=8时,$\stackrel{∧}{y}$=$\frac{5}{2}$×8-3=17,
则|17-16|<2;
由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,
所以得到的线性回归直线方程是可靠的.
点评 本题考查了回归直线方程的计算与应用问题,是基础题目.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案| A. | $\sqrt{6}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
| A. | (-∞,1) | B. | (1,+∞) | C. | (2,+∞) | D. | (-∞,2) |
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
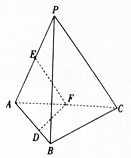 如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,∠BAC=60°,E,F分别是AP,AC的中点,点D在棱AB上,且AD=AC.求证:
如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,∠BAC=60°,E,F分别是AP,AC的中点,点D在棱AB上,且AD=AC.求证: