题目内容
16.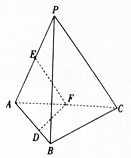 如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,∠BAC=60°,E,F分别是AP,AC的中点,点D在棱AB上,且AD=AC.求证:
如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,∠BAC=60°,E,F分别是AP,AC的中点,点D在棱AB上,且AD=AC.求证:(1)EF∥平面PBC;
(2)DF⊥平面PAC.
分析 (1)利用三角形中位线定理推导出EF∥PC,由此能证明EF∥平面PBC.
(2)由已知条件推导出△ACD为正三角形,DF⊥AC,从而得到DF⊥平面PAC.
解答  (本题满分为12分)
(本题满分为12分)
证明:(1)在△PAC中,因为E,F分别是AP,AC的中点,
所以EF∥PC.…(2分)
又因为EF?平面PBC,PC?平面PBC,
所以EF∥平面PBC.…(5分)
(2)连结CD.因为∠BAC=60°,AD=AC,
所以△ACD为正三角形.
因为F是AC的中点,所以DF⊥AC.…(7分)
因为平面PAC⊥平面ABC,DF?平面ABC,
平面PAC∩平面ABC=AC,
所以DF⊥平面PAC. …(12分)
点评 本题考查直线与平面平行的证明,考查平面与平面垂直的证明,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.设f(x)是定义在R上周期为2的函数,且对任意的实数x,恒有f(x)-f(-x)=0,当x∈[0,1]时,f(x)=-$\sqrt{1-{x^2}}$,则函数g(x)=f(x)-ex+1在区间[-2017,2017]上零点的个数为( )
| A. | 2016 | B. | 2017 | C. | 4032 | D. | 4034 |
11.设a+b<0,且b>0,则下列不等式正确的是( )
| A. | b2>-ab | B. | a2<-ab | C. | a2<b2 | D. | a2>b2 |
1.在一次对昼夜温差大小与种子发芽数之间的研究中,研究人员获得了一组样本数据:
(1)请根据上述数据,选取其中的前3组数据,求出y关于x的线性回归方程;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归直线方程是可靠的,请问(1)中所得的线性回归方程是否可靠?
| 温差x(℃) | 13 | 12 | 11 | 10 | 8 |
| 发芽数y(颗) | 30 | 26 | 25 | 23 | 16 |
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归直线方程是可靠的,请问(1)中所得的线性回归方程是否可靠?
8.已知函数f(x)=$\left\{\begin{array}{l}2x-1,x>0\\ x+1,x≤0\end{array}$,若f(a)=f(1),则实数a的值等于( )
| A. | 0 | B. | 1 | C. | 0或1 | D. | 0或-1 |