题目内容
13.实数x,y满足$\left\{\begin{array}{l}x-y+1≥0\\ x+2y-3≥0\\ 2x+y-6≤0\end{array}\right.$,若2x-y≥m恒成立,则实数m的取值范围是(-∞,-$\frac{2}{3}$].分析 首先画出可行域,由2x-y≥m恒成立,即求2x-y的最小值,设z=2x-y,利用其几何意义求最小值
解答 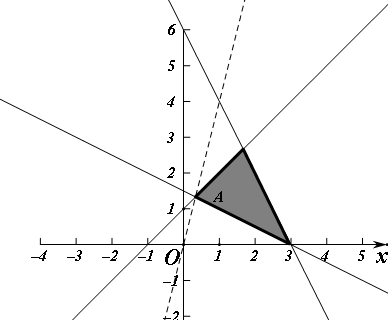 解:x,y满足的平面区域如图:
解:x,y满足的平面区域如图:
设z=2x-y,则y=2x-z,
当经过图中的A时z最小,由$\left\{\begin{array}{l}{x-y+1=0}\\{x+2y-3=0}\end{array}\right.$,
得A($\frac{1}{3},\frac{4}{3}$).
所以z的最小值为2×$\frac{1}{3}$-$\frac{4}{3}$=-$\frac{2}{3}$
所以实数m的取值范围是
(-∞,-$\frac{2}{3}$];
故答案为:(-∞,-$\frac{2}{3}$].
点评 本题考查了简单线性规划问题;正确画出可行域,将恒成立问题求参数范围问题,转化为求4x-y的最小值,属于基础题.

练习册系列答案
相关题目
1.在一次对昼夜温差大小与种子发芽数之间的研究中,研究人员获得了一组样本数据:
(1)请根据上述数据,选取其中的前3组数据,求出y关于x的线性回归方程;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归直线方程是可靠的,请问(1)中所得的线性回归方程是否可靠?
| 温差x(℃) | 13 | 12 | 11 | 10 | 8 |
| 发芽数y(颗) | 30 | 26 | 25 | 23 | 16 |
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归直线方程是可靠的,请问(1)中所得的线性回归方程是否可靠?
8.已知函数f(x)=$\left\{\begin{array}{l}2x-1,x>0\\ x+1,x≤0\end{array}$,若f(a)=f(1),则实数a的值等于( )
| A. | 0 | B. | 1 | C. | 0或1 | D. | 0或-1 |
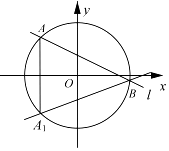 在平面直角坐标系xOy中,已知圆C:x2+y2=4和动直线l:x=my+1.
在平面直角坐标系xOy中,已知圆C:x2+y2=4和动直线l:x=my+1.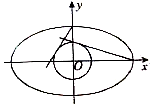 如图,过椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>1)上顶点和右顶点分别作圆x2+y2=1的两条切线的斜率之积为-$\frac{{\sqrt{2}}}{2}$,则椭圆的离心率的取值范围是$({0,\frac{{\sqrt{2}}}{2}})$.
如图,过椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>1)上顶点和右顶点分别作圆x2+y2=1的两条切线的斜率之积为-$\frac{{\sqrt{2}}}{2}$,则椭圆的离心率的取值范围是$({0,\frac{{\sqrt{2}}}{2}})$.