题目内容
9.已知函数f(x)=ax+$\frac{2a-1}{x}$+1-3a(a>0).(Ⅰ)当a=1时,求函数y=f(x)在点(2,f(2))处的切线方程(写成一般式).
(Ⅱ)若不等式f(x)≥(1-a)lnx在x∈[1,+∞)时恒成立,求实数a的取值范围.
分析 (Ⅰ)当a=1时,求导数,确定切线的斜率,即可求出切线方程;
(Ⅱ)记g(x)=ax+$\frac{2a-1}{x}$+1-3a-(1-a)lnx,分类讨论,利用g′(x)≥0在x∈[1,+∞)时恒成立,即可得出结论.
解答 解:(Ⅰ)当a=1时,f(x)=x+$\frac{1}{x}$-2,f′(x)=1-$\frac{1}{{x}^{2}}$,
∴f′(2)=$\frac{3}{4}$,f(2)=$\frac{1}{2}$,
∴函数y=f(x)在点(2,f(2))处的切线方程为y-$\frac{1}{2}$=$\frac{3}{4}$(x-2),即3x-4y-4=0;
(Ⅱ)记g(x)=ax+$\frac{2a-1}{x}$+1-3a-(1-a)lnx,g′(x)=$\frac{a(x-1)[x-(\frac{1}{a}-2)]}{{x}^{2}}$,
0$<a<\frac{1}{3}$时,g′(x)>0,得x>$\frac{1}{a}$-2,令g′(x)<0,得1<x<$\frac{1}{a}$-2,
∴g(x)在(1,$\frac{1}{a}$-2)上是减函数,
∴x∈(1,$\frac{1}{a}$-2),g(x)<g(1)=0,与g(x)≥0在x∈[1,+∞)时恒成立矛盾;
a≥$\frac{1}{3}$,g′(x)≥0在x∈[1,+∞)时恒成立,g(x)在[1,+∞)为增函数,
∴g(x)≥g(1)=0,符合题意,
综上所述,a≥$\frac{1}{3}$
点评 本题考查导数知识的综合运用,考查导数的几何意义,考查分类讨论的数学思想,属于中档题.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
19.在△ABC中,角A、B、C所对的边长分别为a,b,c,如果sin2B=sinAsinC,且c=2a则cosB的值等于( )
| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{\sqrt{2}}{3}$ |
14.已知函数f(x)=ax3+bx2+cx+d的图象如图所示,则下列结论正确的是( )


| A. | a>0,c<0,d>0 | B. | a>0,c>0,d<0 | C. | a<0,c<0,d<0 | D. | a<0,c>0,d<0 |
1.在一次对昼夜温差大小与种子发芽数之间的研究中,研究人员获得了一组样本数据:
(1)请根据上述数据,选取其中的前3组数据,求出y关于x的线性回归方程;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归直线方程是可靠的,请问(1)中所得的线性回归方程是否可靠?
| 温差x(℃) | 13 | 12 | 11 | 10 | 8 |
| 发芽数y(颗) | 30 | 26 | 25 | 23 | 16 |
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归直线方程是可靠的,请问(1)中所得的线性回归方程是否可靠?
19.某地区2007年至2013年农村居民家庭人均纯收入y(单位:千元)的数据如下表:
y关于t的线性回归方程为y=0.5t+2.3,则a的值为( )
| 年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | a | 5.2 | 5.9 |
| A. | 4.5 | B. | 4.6 | C. | 4.7 | D. | 4.8 |
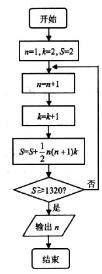 元代数学家朱世杰所著《四元玉鉴》一书,是中国古代数学的重要著作之一,共分卷首、上卷、中卷、下卷四卷,下卷中《果垛叠藏》第一问是:“今有三角垛果子一所,值钱一贯三百二十文,只云从上一个值钱二文,次下层层每个累贯一文,问底子每面几何?”据此,绘制如图所示程序框图,求得底面每边的果子数n为( )
元代数学家朱世杰所著《四元玉鉴》一书,是中国古代数学的重要著作之一,共分卷首、上卷、中卷、下卷四卷,下卷中《果垛叠藏》第一问是:“今有三角垛果子一所,值钱一贯三百二十文,只云从上一个值钱二文,次下层层每个累贯一文,问底子每面几何?”据此,绘制如图所示程序框图,求得底面每边的果子数n为( )
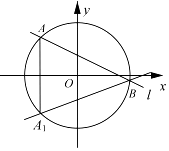 在平面直角坐标系xOy中,已知圆C:x2+y2=4和动直线l:x=my+1.
在平面直角坐标系xOy中,已知圆C:x2+y2=4和动直线l:x=my+1.