题目内容
已知定义在{x|x≠0,x∈R}上的函数f(x)满足对于任意的x1,x2,有f(x1•x2)=f(x1)+f(x2)
(1)求f(1)和f(-1);
(2)判断函数f(x)的奇偶性,并证明你的结论;
(3)如果f(
)=1,且f(x)在(0,+∞)上是增函数,问是否存在正实数a,使f(x)+f(x-a)≤2在区间[1-a,1+a]上恒成立,若存在,试求出a的取值范围,若不存在,说明理由.
(1)求f(1)和f(-1);
(2)判断函数f(x)的奇偶性,并证明你的结论;
(3)如果f(
| 6 |
考点:函数恒成立问题,函数奇偶性的判断
专题:函数的性质及应用,不等式的解法及应用
分析:(1)在f(x1•x2)=f(x1)+f(x2)中取x1=x2=1即可求得f(1)=0.取x1=x2=-1可得f(-1)=0;
(2)在f(x1•x2)=f(x1)+f(x2)中取x1=x,x2=-1可证得f(x)是偶函数;
(3)由区间[1-a,1+a],得1+a≥1-a求得a≥0;f(x)在x=0无定义得1-a>0,即a<1;由1-a≤x≤1+a得1-2a≤x-a≤1;根据f(x-a)在x=a无定义得1-2a>0,即a<
;最后得0≤a<
.再由f(
)=1,得f(6)=2,进一步得到f[x(x-a)]≤f(6),由在(0,+∞)上f(x)为增函数得x(x-a)≤6,分析可知
<0、
>
,由1-a≤x≤1+a及0≤a<
,知0<
<x<
<
,得到当0≤a<
和x∈[1-a,1+a]时,恒满足x(x-a)≤6,则可得
当0≤a<
时,在区间[1-a,1+a],不等式f(x)+f(x-a)≤2恒成立.
(2)在f(x1•x2)=f(x1)+f(x2)中取x1=x,x2=-1可证得f(x)是偶函数;
(3)由区间[1-a,1+a],得1+a≥1-a求得a≥0;f(x)在x=0无定义得1-a>0,即a<1;由1-a≤x≤1+a得1-2a≤x-a≤1;根据f(x-a)在x=a无定义得1-2a>0,即a<
| 1 |
| 2 |
| 1 |
| 2 |
| 6 |
a-
| ||
| 2 |
a+
| ||
| 2 |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 6 |
| 1 |
| 2 |
当0≤a<
| 1 |
| 2 |
解答:
解:(1)将x1=x2=1代入f(x1•x2)=f(x1)+f(x2),
得f(1)=f(1)+f(1),即f(1)=0.
将x1=x2=-1代入f(x1•x2)=f(x1)+f(x2),
得f(1)=2f(-1),∴f(-1)=0;
(2)f(x)是偶函数.
事实上,在f(x1•x2)=f(x1)+f(x2)中,
取x1=x,x2=-1,得
f(-x)=f(-1)+f(x)=f(x),
∴f(x)是偶函数;
(3)对区间[1-a,1+a],应有1+a≥1-a,
∴a≥0 ①.
∵f(x)在x=0无定义,∴1-a>0,即a<1 ②.
综合①和②得0≤a<1 ③.
∵1-a≤x≤1+a,∴1-2a≤x-a≤1,
f(x-a)在x=a无定义,∴1-2a>0,即a<
④.
综合③、④得0≤a<
⑤.
∵f(
)=1,∴f(6)=f(
×
)=f(
)+f(
)=1+1=2;
f(x)+f(x-a)=f[x(x-a)]≤2,即f[x(x-a)]≤f(6),
∵在(0,+∞)上f(x)为增函数,∴x(x-a)≤6,
解此不等式得
≤x≤
⑥.
而
<0、
>
,
由1-a≤x≤1+a及0≤a<
,知0<
<x<
<
,
∴当0≤a<
和x∈[1-a,1+a]时,恒满足⑥式,
即当0≤a<
时,在区间[1-a,1+a],不等式f(x)+f(x-a)≤2恒成立.
得f(1)=f(1)+f(1),即f(1)=0.
将x1=x2=-1代入f(x1•x2)=f(x1)+f(x2),
得f(1)=2f(-1),∴f(-1)=0;
(2)f(x)是偶函数.
事实上,在f(x1•x2)=f(x1)+f(x2)中,
取x1=x,x2=-1,得
f(-x)=f(-1)+f(x)=f(x),
∴f(x)是偶函数;
(3)对区间[1-a,1+a],应有1+a≥1-a,
∴a≥0 ①.
∵f(x)在x=0无定义,∴1-a>0,即a<1 ②.
综合①和②得0≤a<1 ③.
∵1-a≤x≤1+a,∴1-2a≤x-a≤1,
f(x-a)在x=a无定义,∴1-2a>0,即a<
| 1 |
| 2 |
综合③、④得0≤a<
| 1 |
| 2 |
∵f(
| 6 |
| 6 |
| 6 |
| 6 |
| 6 |
f(x)+f(x-a)=f[x(x-a)]≤2,即f[x(x-a)]≤f(6),
∵在(0,+∞)上f(x)为增函数,∴x(x-a)≤6,
解此不等式得
a-
| ||
| 2 |
a+
| ||
| 2 |
而
a-
| ||
| 2 |
a+
| ||
| 2 |
| 6 |
由1-a≤x≤1+a及0≤a<
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 6 |
∴当0≤a<
| 1 |
| 2 |
即当0≤a<
| 1 |
| 2 |
点评:本题考查了函数奇偶性的性质,考查了函数恒成立问题,(3)的求解,综合考查了学生的逻辑思维及抽象思维的能力,是压轴题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
已知全集U=R,集合A={x|2x>1},B={x|log2x>2},则A∩B=( )
| A、{x|x>0} |
| B、{x|x<-1或x>0} |
| C、{x|x>4} |
| D、{x|-1≤x≤4} |
已知函数y=f(x)的图象如图,则满足f(
)•f(5)≤0的x取值范围为( )
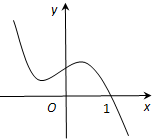
| 2x+1 |
| x-1 |

| A、[-2,1) |
| B、[-1,1] |
| C、[1,2] |
| D、[2,3] |
已知如图程序框图,则输出的i是( )


| A、9 | B、11 | C、13 | D、15 |
设{an}是由正数组成的等比数列,Sn为其前n项和.已知a2a4=1,S3=7,则S5=( )
A、
| ||
B、
| ||
C、
| ||
D、
|