题目内容
已知sinx+siny=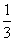 ,求sinx-cos2y的最大、最小值.
,求sinx-cos2y的最大、最小值.
由sinx=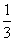 -siny及-1≤sinx≤1得,
-siny及-1≤sinx≤1得,
- ≤siny≤1.
≤siny≤1.
而sinx-cos2y=sin2y-siny-
=(siny- )2-
)2- ,
,
所以当siny= 时,最小值为-
时,最小值为- ,
,
当siny=- 时,最大值为
时,最大值为 .
.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
某公司今年1月份推出新产品A,其成本价为492元/件,经试销调查,销售量与销售价的关系如下表:
| 销售价x(元/件) | 650 | 662 | 720 | 800 |
| 销售量y(件) | 350 | 333 | 281 | 200 |
由此可知,销售量y(件)与销售价x(元/件)可近似看作一次函数y=kx+b的关系(通常取表中相距较远的两组数据所得的一次函数较为精确).
试问:销售价定为多少时,1月份利润最大?并求最大利润和此时的销售量.
 )=
)= ,则sin(2α+
,则sin(2α+ )的值为________.
)的值为________. =________.
=________.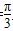 ,a=
,a= ,b=1,则c等于( )
,b=1,则c等于( ) ,且
,且 =-27.
=-27. ,λ∈R,若
,λ∈R,若 =-
=- ,则λ=( )
,则λ=( ) B.
B.
 D.
D.