题目内容
13.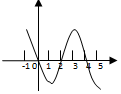 已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数 f′(x)的图象如图所示.
已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数 f′(x)的图象如图所示.| x | -1 | 0 | 4 | 5 |
| f(x) | 1 | 2 | 2 | 1 |
①函数f(x)的值域为[1,2];
②函数f(x)在[0,2]上是减函数;
③若x∈[-1,t]时,f(x)的最大值是2,则t的最大值为4;
④当1<a<2时,函数y=f(x)-a有4个零点
其中是真命题的是②③.
分析 根据导函数值的正负,可以判定函数f(x)的单调性,由表格中的函数值可以判定函数的最值情况.
解答 解:根据导函数值的正负,可以判定函数f(x)在(-1,0),(2,4)递增,
在(0,2),(4,5)递减,
且极小值f(2)未知,所以①错,②正确,③正确,④错;
故答案为:②④
点评 本题考查了函数的性质与其导数的关系,属于基础题.

练习册系列答案
相关题目
13.下列函数中,既是偶函数又存在零点的是( )
| A. | y=x2+1 | B. | y=|lgx| | C. | y=cosx | D. | y=ex-1 |
3.已知函数f(x)对定义域内R内的任意x都有f(x)=f(4-x),且当x≠2时,其导数f'(x)满足xf'(x)>2f'(x),若2<a<4,则( )
| A. | $f({2^x})<f(\frac{lna}{a})<f[{(\frac{lna}{a})^2}]$ | B. | $f(\frac{lna}{a})<f[{(\frac{lna}{a})^2}]<f({2^x})$ | ||
| C. | $f(\frac{lna}{a})<f({2^x})<f[{(\frac{lna}{a})^2}]$ | D. | $f({2^x})<f[{(\frac{lna}{a})^2}]<f(\frac{lna}{a})$ |