题目内容
8．若$z=\frac{{{{（1+i）}^4}{{（-1-\sqrt{3}i）}^7}}}{{{{（1-i）}^{12}}}}$，则|z|=8．分析 利用复数的运算法则、棣莫佛定理即可得出．
解答 解：∵（1+i）4=（2i）2=-4，（1-i）12=[（1-i）2]6=（-2i）6=-64．
$（-1-\sqrt{3}i）^{7}$=$（-2）^{7}（cos\frac{π}{3}+isin\frac{π}{3}）^{7}$=-128×$（cos\frac{7π}{3}+isin\frac{7π}{3}）$=-128$（\frac{1}{2}+\frac{\sqrt{3}}{2}i）$=-64$（1+\sqrt{3}i）$．
∴z=$\frac{-4×[-64（1+\sqrt{3}i）]}{-64}$=-4-4$\sqrt{3}$i．
∴|z|=$\sqrt{{4}^{2}+（-4\sqrt{3}）^{2}}$=8．
故答案为：8．
点评 本题考查了复数的运算法则、棣莫佛定理，考查了推理能力与计算能力，属于中档题．
练习册系列答案
优百分课时互动系列答案
开心蛙状元作业系列答案
相关题目
8．已知双曲线：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左右焦点分别为F1，F2，点P为双曲线右支上一点，若|PF1|2=8a|PF2|，则双曲线离心率的取值范围是（ ）
| A． | （1，3] | B． | [3，+∞） | C． | （0，3） | D． | （0，3] |
13．
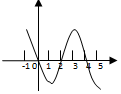已知函数f（x）的定义域为[-1，5]，部分对应值如下表，f（x）的导函数 f′（x）的图象如图所示．
下列关于函数f（x）的命题：
①函数f（x）的值域为[1，2]；
②函数f（x）在[0，2]上是减函数；
③若x∈[-1，t]时，f（x）的最大值是2，则t的最大值为4；
④当1＜a＜2时，函数y=f（x）-a有4个零点
其中是真命题的是②③．
已知函数f（x）的定义域为[-1，5]，部分对应值如下表，f（x）的导函数 f′（x）的图象如图所示．| x | -1 | 0 | 4 | 5 |
| f（x） | 1 | 2 | 2 | 1 |
①函数f（x）的值域为[1，2]；
②函数f（x）在[0，2]上是减函数；
③若x∈[-1，t]时，f（x）的最大值是2，则t的最大值为4；
④当1＜a＜2时，函数y=f（x）-a有4个零点
其中是真命题的是②③．
20．若sinα=$\frac{\sqrt{3}}{3}$，则cos2α=（ ）
| A． | $-\frac{2}{3}$ | B． | $-\frac{1}{3}$ | C． | $\frac{1}{3}$ | D． | $\frac{2}{3}$ |