题目内容
4．函数y=2x-2+7的图象恒过定点A，且点A在幂函数f（x）的图象上，则f（3）=27．分析 根据指数函数的图象恒过定点A（0，1）求出点A的坐标，
再代入幂函数解析式求出f（x）的解析式，计算f（3）的值．
解答 解：当x-2=0时，x=2，y=2°+7=8；
∴函数y=2x-2+7的图象恒过定点A（2，8）；
又点A在幂函数f（x）=xα的图象上，
∴2α=8，解得α=3；
∴f（x）=x3，
∴f（3）=33=27．
故答案为：27．
点评 本题考查了指数函数、幂函数的图象与性质的应用问题，是基础题目．
练习册系列答案
怎样学好牛津英语系列答案
导学教程高中新课标系列答案
相关题目
4．已知实数x，y满足$\left\{\begin{array}{l}{x≥0}\\{x-2y≥0}\\{y≥x-1}\end{array}\right.$，则z=ax+y（a＞0）的最小值为（ ）
| A． | 0 | B． | a | C． | 2a+1 | D． | -1 |
5．已知函数f（x）=cos（ωx-$\frac{ωπ}{6}$）（ω＞0）的最小正周期为π，则函数f（x）的图象（ ）
| A． | 可由函数g（x）=cos2x的图象向左平移$\frac{π}{3}$个单位而得 | |
| B． | 可由函数g（x）=cos2x的图象向右平移$\frac{π}{3}$个单位而得 | |
| C． | 可由函数g（x）=cos2x的图象向左平移$\frac{π}{6}$个单位而得 | |
| D． | 可由函数g（x）=cos2x的图象向右平移$\frac{π}{6}$个单位而得 |
13．
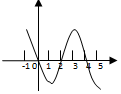已知函数f（x）的定义域为[-1，5]，部分对应值如下表，f（x）的导函数 f′（x）的图象如图所示．
下列关于函数f（x）的命题：
①函数f（x）的值域为[1，2]；
②函数f（x）在[0，2]上是减函数；
③若x∈[-1，t]时，f（x）的最大值是2，则t的最大值为4；
④当1＜a＜2时，函数y=f（x）-a有4个零点
其中是真命题的是②③．
已知函数f（x）的定义域为[-1，5]，部分对应值如下表，f（x）的导函数 f′（x）的图象如图所示．| x | -1 | 0 | 4 | 5 |
| f（x） | 1 | 2 | 2 | 1 |
①函数f（x）的值域为[1，2]；
②函数f（x）在[0，2]上是减函数；
③若x∈[-1，t]时，f（x）的最大值是2，则t的最大值为4；
④当1＜a＜2时，函数y=f（x）-a有4个零点
其中是真命题的是②③．