题目内容
2.${C}_{n}^{o}$+${C}_{n+1}^{1}$+${C}_{n+2}^{2}$+…+${C}_{n+m-1}^{m-1}$=${C}_{n+m}^{m-1}$.分析 利用组合数公式${C}_{n}^{m}$+${C}_{n}^{m-1}$=${C}_{n+1}^{m}$,进行化简即可.
解答 解:${C}_{n}^{o}$+${C}_{n+1}^{1}$+${C}_{n+2}^{2}$+…+${C}_{n+m-1}^{m-1}$=${C}_{n+1}^{0}$+${C}_{n+1}^{1}$+${C}_{n+2}^{2}$+…+${C}_{n+m-1}^{m-1}$
=${C}_{n+2}^{1}$+${C}_{n+2}^{2}$+…+${C}_{n+m-1}^{m-1}$
=${C}_{n+3}^{2}$+…+${C}_{n+m-1}^{m-1}$
=…=${C}_{n+m-1}^{m-2}$+${C}_{n+m-1}^{m-1}$
=${C}_{n+m}^{m-1}$.
故答案为:${C}_{n+m}^{m-1}$.
点评 本题考查了组合数公式的应用问题,也考查了逻辑思维与推理能力,是基础题目.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
12.求证:$\frac{si{n}^{2}x}{1+cotx}$+$\frac{co{s}^{2}x}{1+tanx}$=1-sinxcosx.[提示:a3+b3=(a+b)(a2-ab+b2)].
11.若点P(1,1)在圆x2+y2+2x+4y+a=0外,则a的取值范围是( )
| A. | a<-8 | B. | a>-8 | C. | -8<a<5 | D. | a<-8或a>5 |
17. 某校为了调查“学业水平考试”学生的数学成绩,随机地抽取该校甲、乙两班各10名同学,获得的数据如下:(单位:分)
某校为了调查“学业水平考试”学生的数学成绩,随机地抽取该校甲、乙两班各10名同学,获得的数据如下:(单位:分)
(1)以百位和十位为茎,个位为叶,在图中作出甲、乙两班学生数学成绩的茎叶图,并判列哪个班的平均水平较高;
(2)若数学成绩不低于128分,称为“优秀”,求从甲班这10名学生中随机选取3名,至多有1名“优秀”的概率.
(3)以这20人的样本数据来估计整个学校的总体成绩,若从该校(人数很多)任选3人,记X表示抽到“优秀”学生的人数,求X的数学期望.
 某校为了调查“学业水平考试”学生的数学成绩,随机地抽取该校甲、乙两班各10名同学,获得的数据如下:(单位:分)
某校为了调查“学业水平考试”学生的数学成绩,随机地抽取该校甲、乙两班各10名同学,获得的数据如下:(单位:分)| 甲 | 132 | 108 | 112 | 121 | 113 | 121 | 118 | 127 | 118 | 129 |
| 乙 | 133 | 107 | 120 | 113 | 122 | 114 | 125 | 118 | 129 | 127 |
(2)若数学成绩不低于128分,称为“优秀”,求从甲班这10名学生中随机选取3名,至多有1名“优秀”的概率.
(3)以这20人的样本数据来估计整个学校的总体成绩,若从该校(人数很多)任选3人,记X表示抽到“优秀”学生的人数,求X的数学期望.
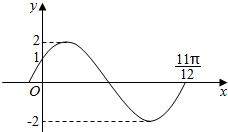 如图所示为函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象.
如图所示为函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象.