题目内容
已知Sn是等比数列{an}的前n项和，如果a3+a6=2，a4a5=-8，且a3＜a6，则
=（ ）
| S9 |
| S6 |
| A、4 | B、3 | C、-3 | D、-4 |
考点：等比数列的性质
专题：计算题,等差数列与等比数列
分析：利用已知条件求出等比数列的公比，然后求解表达式的值．
解答：
解：Sn是等比数列{an}的前n项和，如果a3+a6=2，a4a5=-8，且a3＜a6，
∴a3+a6=2，a3a6=-8，且a3＜a6，
∴a3=-2，a6=4，∴q3=-2，
∴
=
=-3
故选：C．
∴a3+a6=2，a3a6=-8，且a3＜a6，
∴a3=-2，a6=4，∴q3=-2，
∴
| S9 |
| S6 |
| 1-(-2)9 |
| 1-(-2)6 |
故选：C．
点评：本题考查等比数列的前n项和，考查等比数列的性质，考查学生的计算能力，熟练利用等比数列的性质解题可以简化计算过程，给解题带来方便．
练习册系列答案
相关题目
集合P中的元素都是整数，并且满足条件：
①P中有正数，也有负数；
②P中有奇数，也有偶数；
③-1∉P；
④若x，y∈P，则x+y∈P．
下面判断正确的是（ ）
①P中有正数，也有负数；
②P中有奇数，也有偶数；
③-1∉P；
④若x，y∈P，则x+y∈P．
下面判断正确的是（ ）
| A、0∉P，2∈P |
| B、0∈P，2∈P |
| C、0∈P，2∉P |
| D、0∉P，2∉P |
问题：有1000个乒乓球分别装在3个箱子里，其中红色箱子内有500个，蓝色箱子内有200个，黄色箱子内有300个，现从中抽取一个容量为100的样本：方法Ⅰ：随机抽样法Ⅱ：系统抽样法Ⅲ：分层抽样法．其中问题与方法能配对的是（ ）
| A、Ⅰ | B、Ⅱ | C、Ⅲ | D、Ⅱ或Ⅲ |
已知集合A={x|y=lnx-2012}，集合B={-2，-1，1，2}，则A∩B=（ ）
| A、φ |
| B、{1，2} |
| C、{-1，-2} |
| D、{-2，-1，1，2} |
已知p：（x-1）（x-2）≤0，q：log2（x+1）≤2，则p是q的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
数列{an}的通项公式为an=4n-1，则bk=
（a1+a2+…+ak）（k∈N*）所确定的数列{bn}的前n项和为（ ）
| 1 |
| k |
| A、n2 |
| B、n（n+1） |
| C、n（n+2） |
| D、n（2n+1） |
已知点A（2，-1），B（4，2），点P在x轴上，当
•
取最小值时，P点的坐标是（ ）
| PA |
| PB |
| A、（2，0） | ||
| B、（4，0） | ||
C、（
| ||
| D、（3，0） |
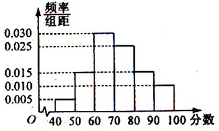我校从高一年级学生中随机抽取部分学生，将他们的数学竞赛成绩分为6组：[40，50），[50，60），[60，70），[70，80），[80，90），[90，100）加以统计，得到如图所示的频率分布直方图．