题目内容
在△ABC中，D为AB上任一点，h为AB边上的高，△ADC、△BDC、△ABC的内切圆半径分别为r1，r2，r，则有如下的等式恒成立：
+
=
+
，三棱锥P-ABC中D位AB上任一点，h为过点P的三棱锥的高，三棱锥P-ADC、P-BDC、P-ABC的内切球的半径分别为r1，r2，r，请类比平面三角形中的结论，写出类似的一个恒等式为
+
=
+
+
=
+
．
| AC |
| r1 |
| BD |
| r2 |
| AB |
| r |
| 2CD |
| h |
| S△ADC |
| r1 |
| S△BCD |
| r2 |
| S△ABC |
| r |
| 2S△PDC |
| h |
| S△ADC |
| r1 |
| S△BCD |
| r2 |
| S△ABC |
| r |
| 2S△PDC |
| h |
分析：本题是根据三角形类比三棱锥，二维是线段，三维应该是面积，故把等式
+
=
+
中的线段替换成相对应的面积即可．
| AC |
| r1 |
| BD |
| r2 |
| AB |
| r |
| 2CD |
| h |
解答：解：本题是根据三角形类比三棱锥，显然给出的半径是一致的，均为r1，r2，r，不同的是分子，而不再是线段了，二维是线段，三维应该是面积，故把等式
+
=
+
中的线段替换成相对应的面积即可，于是得到
+
=
+
．
故答案为：
+
=
+
| AC |
| r1 |
| BD |
| r2 |
| AB |
| r |
| 2CD |
| h |
| S△ADC |
| r1 |
| S△BCD |
| r2 |
| S△ABC |
| r |
| 2S△PDC |
| h |
故答案为：
| S△ADC |
| r1 |
| S△BCD |
| r2 |
| S△ABC |
| r |
| 2S△PDC |
| h |
点评：本题考查类比推理，考查学生分析解决问题的能力，掌握类比推理的方法是关键．
练习册系列答案
相关题目
在△ABC中，D为AB上一点，M为△ABC内一点，且满足
=
，
=
+
，则△AMD与△ABC的面积比为（ ）
| AD |
| 3 |
| 4 |
| AB |
| AM |
| AD |
| 3 |
| 5 |
| BC |
A、
| ||
B、
| ||
C、
| ||
D、
|
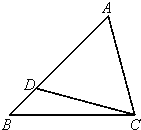如图，在△ABC中，D为边AB上一点，DA=DC．已知B=