题目内容
函数f（x）的导函数f′（x）的图象如图所示，那么f（x）的图象最有可能的是（ ）
A、 |
B、 |
C、 |
D、 |
考点：利用导数研究函数的单调性
专题：导数的概念及应用
分析：由图象得出函数的单调性，从而选出正确选项．
解答：
解：由图象得：
在（-∞，-2）上，f′（x）＜0，f（x）递减，
在（-2，-1）上，f′（x）＞0，f（x）递增，
在（-1，+∞）上，f′（x）＜0，f（x）递减，
故选：B．
在（-∞，-2）上，f′（x）＜0，f（x）递减，
在（-2，-1）上，f′（x）＞0，f（x）递增，
在（-1，+∞）上，f′（x）＜0，f（x）递减，
故选：B．
点评：本题考察了函数的单调性，导数的应用，渗透了数形结合思想，是一道基础题．
练习册系列答案
全能测控一本好卷系列答案
发散思维新课堂系列答案
相关题目
若命题“￢（p∨q）”为真命题，则（ ）
| A、p，q均为假命题 |
| B、p，q中至多有一个为真命题 |
| C、p，q均为真命题 |
| D、p，q中至少有一个为真命题 |
如图所示，l1∥l2∥l3，下列比例式正确的是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在-2π～0内与
π终边相同的角是（ ）
| 52 |
| 7 |
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
函数y=
x2-lnx的单调减区间是（ ）注：（lnx）′=
．
| 1 |
| 2 |
| 1 |
| x |
| A、（-∞，-1） |
| B、（0，1）∪（-∞，-1） |
| C、（0，1） |
| D、（-∞，+∞） |
若（a+2i）i=b+i，其中a，b∈R，i是虚数单位，则a-b=（ ）
| A、-3 | B、-2 | C、2 | D、3 |
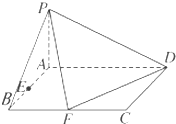已知四棱锥P-ABCD底面ABCD是矩形PA⊥平面ABCD，AD=2，AB=1，E、F分别是线段AB，BC的中点，