题目内容
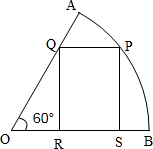 如图,已知扇形AOB的半径为1,中心角为60°,四边形PQRS是扇形的内接矩形,P为
如图,已知扇形AOB的半径为1,中心角为60°,四边形PQRS是扇形的内接矩形,P为 |
| AB |
考点:已知三角函数模型的应用问题
专题:计算题,解三角形
分析:如图先用所给的角将矩形的面积表示出来,建立三角函数模型,再根据所建立的模型利用三角函数的性质求最值.
解答:
解:如图,在Rt△OPS中,设∠POS=α,则OS=cosα,PS=sinα,
在Rt△ORQ中,
=tan60°=
,所以OR=
QR=
sinα.
∴RS=OS-OR=cosα-
sinα.
设矩形ABCD的面积为S,则S=RS•BRQ=(cosα-
sinα)sinα
=sinαcosα-
sin2α
=
sin2α+
cos2α-
=
(
sin2α+
cos2α)-
=
sin(2α+
)-
.
由于0<α<
,所以当2α+
=
,即α=
时,S最大=
-
=
.
因此,当α=
时,矩形ABCD的面积最大,最大面积为
.

在Rt△ORQ中,
| QR |
| OR |
| 3 |
| ||
| 3 |
| ||
| 3 |
∴RS=OS-OR=cosα-
| ||
| 3 |
设矩形ABCD的面积为S,则S=RS•BRQ=(cosα-
| ||
| 3 |
=sinαcosα-
| ||
| 3 |
=
| 1 |
| 2 |
| ||
| 6 |
| ||
| 6 |
=
| ||
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 6 |
=
| ||
| 3 |
| π |
| 6 |
| ||
| 6 |
由于0<α<
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| ||
| 3 |
| ||
| 6 |
| ||
| 6 |
因此,当α=
| π |
| 6 |
| ||
| 6 |
点评:本题考查在实际问题中建立三角函数模型,求解问题的关键是根据图形建立起三角模型,将三角模型用所学的恒等式变换公式进行化简.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
若α、β为锐角,则下列不等式中一定成立的是( )
| A、sin(α+β)>sinα+sinβ |
| B、sin(α+β)<sinα+sinβ |
| C、cos(α+β)>cosα+cosβ |
| D、cos(α+β)<sinα+sinβ |