题目内容
若α、β为锐角,则下列不等式中一定成立的是( )
| A、sin(α+β)>sinα+sinβ |
| B、sin(α+β)<sinα+sinβ |
| C、cos(α+β)>cosα+cosβ |
| D、cos(α+β)<sinα+sinβ |
考点:两角和与差的正弦函数,两角和与差的余弦函数
专题:三角函数的图像与性质
分析:根据两角和的正弦公式即可得到结论.
解答:
解:sin(α+β)=sinαcosβ+cosαsinβ,
∵α、β为锐角,
∴0<cosβ<1,0<cosα<1,
∴sinαcosβ+cosαsinβ<sinα+sinβ,
∴sin(α+β)<sinα+sinβ成立,
故选:B.
∵α、β为锐角,
∴0<cosβ<1,0<cosα<1,
∴sinαcosβ+cosαsinβ<sinα+sinβ,
∴sin(α+β)<sinα+sinβ成立,
故选:B.
点评:本题主要考查两角和的正弦公式的应用,以及利用正弦函数和余弦函数的有界性是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知圆锥的全面积是底面积的5倍,那么该圆锥的侧面展开图的圆心角为( )
| A、120° | B、180° |
| C、90° | D、150° |
已知∠B是△ABC的一个内角,下列函数能取负值的是( )
| A、sinB | ||
| B、cosB | ||
C、tan
| ||
D、cos
|
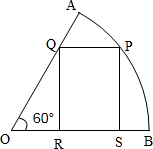 如图,已知扇形AOB的半径为1,中心角为60°,四边形PQRS是扇形的内接矩形,P为
如图,已知扇形AOB的半径为1,中心角为60°,四边形PQRS是扇形的内接矩形,P为