题目内容
已知函数f(x)=4x+
+b(a,b∈R)为奇函数.
(Ⅰ)若f(1)=5,求函数f(x)的解析式;
(Ⅱ)当a=-2时,不等式f(x)≤t在[1,4]上恒成立,求实数t的最小值;
(Ⅲ)当a≥1时,求证:函数g(x)=f(2x)-c(c∈R)在(-∞,-1]上至多有一个零点.
| a |
| x |
(Ⅰ)若f(1)=5,求函数f(x)的解析式;
(Ⅱ)当a=-2时,不等式f(x)≤t在[1,4]上恒成立,求实数t的最小值;
(Ⅲ)当a≥1时,求证:函数g(x)=f(2x)-c(c∈R)在(-∞,-1]上至多有一个零点.
考点:利用导数求闭区间上函数的最值,函数奇偶性的性质
专题:综合题,函数的性质及应用
分析:(Ⅰ)由奇函数定义可得f(-x)=-f(x),可求b,由f(1)=5可得a;
(Ⅱ)不等式f(x)≤t在[1,4]上恒成立,等价于f(x)max≤t,易判断a=-2时f(x)在[1,4]上的单调性,由单调性可得最大值;
(Ⅲ)表示出g(x),只需判定函数g(x)在(-∞,-1]单调即可,利用单调性的定义可作出判断;
(Ⅱ)不等式f(x)≤t在[1,4]上恒成立,等价于f(x)max≤t,易判断a=-2时f(x)在[1,4]上的单调性,由单调性可得最大值;
(Ⅲ)表示出g(x),只需判定函数g(x)在(-∞,-1]单调即可,利用单调性的定义可作出判断;
解答:
解:(Ⅰ)∵函数f(x)=4x+
+b(a,b∈R)为奇函数,
∴f(-x)=-f(x),即-4x-
+b=-4x-
-b,
∴b=0,
又f(1)=4+a+b=5,
∴a=1
∴函数f(x)的解析式为f(x)=4x+
.
(Ⅱ)a=-2,f(x)=4x-
.
∵函数y=4x,y=-
在[1,4]均单调递增,
∴函数f(x)在[1,4]单调递增,
∴当x∈[1,4]时,f(x)max=f(4)=
.
∵不等式f(x)≤t在[1,4]上恒成立,
∴t≥
,
∴实数t的最小值为
.
(Ⅲ)证明:g(x)=4•2x+
-c,
设x1<x2≤-1,
=
,
∵x1<x2≤-1,
∴x1+x2<-2,4•2x1+x2<4•2-2=1,
∵a≥1,即-a≤-1,
∴4•2x1+x2-a<0,又2x1-2x2<0,2x1+x2>0,
∴g(x1)-g(x2)>0,即g(x1)>g(x2),
∴函数g(x)在(-∞,-1]单调递减,
又c∈R,可知函数g(x)在(-∞,-1]上至多有一个零点.
| a |
| x |
∴f(-x)=-f(x),即-4x-
| a |
| x |
| a |
| x |
∴b=0,
又f(1)=4+a+b=5,
∴a=1
∴函数f(x)的解析式为f(x)=4x+
| 1 |
| x |
(Ⅱ)a=-2,f(x)=4x-
| 2 |
| x |
∵函数y=4x,y=-
| 2 |
| x |
∴函数f(x)在[1,4]单调递增,
∴当x∈[1,4]时,f(x)max=f(4)=
| 31 |
| 2 |
∵不等式f(x)≤t在[1,4]上恒成立,
∴t≥
| 31 |
| 2 |
∴实数t的最小值为
| 31 |
| 2 |
(Ⅲ)证明:g(x)=4•2x+
| a |
| 2x |
设x1<x2≤-1,
|
=
| (4•2x1+x2-a)(2x1-2x2) |
| 2x1+x2 |
∵x1<x2≤-1,
∴x1+x2<-2,4•2x1+x2<4•2-2=1,
∵a≥1,即-a≤-1,
∴4•2x1+x2-a<0,又2x1-2x2<0,2x1+x2>0,
∴g(x1)-g(x2)>0,即g(x1)>g(x2),
∴函数g(x)在(-∞,-1]单调递减,
又c∈R,可知函数g(x)在(-∞,-1]上至多有一个零点.
点评:本题考查函数的单调性、奇偶性及其应用,考查函数最值的求解,考查学生综合运用函数性质分析解决问题的能力,属中档题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
已知函数f(x)=x2-2ln|x|与g(x)=sin(x+ψ)(ω>0)有两个公共点,则在下列函数中满足条件的周期最大的g(x)等于( )
A、sin(2πx-
| ||||
B、sin(
| ||||
C、sin(πx-
| ||||
D、sin(πx+
|
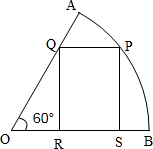 如图,已知扇形AOB的半径为1,中心角为60°,四边形PQRS是扇形的内接矩形,P为
如图,已知扇形AOB的半径为1,中心角为60°,四边形PQRS是扇形的内接矩形,P为