题目内容
在△ABC中,a,b,c分别是角A,B,C的对边,且2cosAcosC(tanAtanC-1)=1.
(Ⅰ)求B的大小;
(Ⅱ)若a+c=
,b=
,求△ABC的面积.
(Ⅰ)求B的大小;
(Ⅱ)若a+c=
3
| ||
| 2 |
| 3 |
考点:余弦定理,三角函数中的恒等变换应用,正弦定理
专题:三角函数的求值
分析:(Ⅰ)已知等式括号中利用同角三角函数间基本关系切化弦,去括号后利用两角和与差的余弦函数公式化简,再由诱导公式变形求出cosB的值,即可确定出B的大小;
(Ⅱ)由cosB,b的值,利用余弦定理列出关系式,再利用完全平方公式变形,将a+b以及b的值代入求出ac的值,再由cosB的值,利用三角形面积公式即可求出三角形ABC面积.
(Ⅱ)由cosB,b的值,利用余弦定理列出关系式,再利用完全平方公式变形,将a+b以及b的值代入求出ac的值,再由cosB的值,利用三角形面积公式即可求出三角形ABC面积.
解答:
解:(Ⅰ)由2cosAcosC(tanAtanC-1)=1得:2cosAcosC(
-1)=1,
∴2(sinAsinC-cosAcosC)=1,即cos(A+C)=-
,
∴cosB=-cos(A+C)=
,
又0<B<π,
∴B=
;
(Ⅱ)由余弦定理得:cosB=
=
,
∴
=
,
又a+c=
,b=
,
∴
-2ac-3=ac,即ac=
,
∴S△ABC=
acsinB=
×
×
=
.
| sinAsinC |
| cosAcosC |
∴2(sinAsinC-cosAcosC)=1,即cos(A+C)=-
| 1 |
| 2 |
∴cosB=-cos(A+C)=
| 1 |
| 2 |
又0<B<π,
∴B=
| π |
| 3 |
(Ⅱ)由余弦定理得:cosB=
| a2+c2-b2 |
| 2ac |
| 1 |
| 2 |
∴
| (a+c)2-2ac-b2 |
| 2ac |
| 1 |
| 2 |
又a+c=
3
| ||
| 2 |
| 3 |
∴
| 27 |
| 4 |
| 5 |
| 4 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
| ||
| 2 |
5
| ||
| 16 |
点评:此题考查了余弦定理,三角形面积公式,两角和与差的余弦函数公式,熟练掌握余弦定理是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
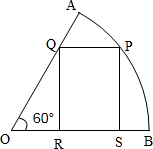 如图,已知扇形AOB的半径为1,中心角为60°,四边形PQRS是扇形的内接矩形,P为
如图,已知扇形AOB的半径为1,中心角为60°,四边形PQRS是扇形的内接矩形,P为
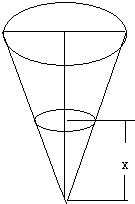 如图,圆锥型量杯口径为2R,高为h,求量杯母线上刻度V(容积)与液面深x的函数关系.
如图,圆锥型量杯口径为2R,高为h,求量杯母线上刻度V(容积)与液面深x的函数关系.