题目内容
已知全集U={x|x=3n,n∈N*,n≤5},集合A={x|x2-px+27=0},集合B={x|x2-15x+q=0},且A∪∁uB={3,9,12,15},求p,q的值.
考点:交、并、补集的混合运算
专题:集合
分析:列举出集合U中的元素,由A与B补集的并集得到3,9,12,15中可能属于A,根据A中方程,利用根与系数的关系求出p的值,确定出6,9属于B,利用根与系数的关系求出q的值即可.
解答:
解:∵全集U={3,6,9,12,15},A∪(∁UB)={3,9,12,15},
∴3,9,12,15中可能有两个属于A,
∵A中的方程x2-px+27=0中,两根之和x1•x2=27,
∴3,9∈A,
∴p=3+9=12,
又∵12,15∉A,
∴12,15∉B,
∵B中的方程x2-15x+q=0中,两根之和x3+x4=15,
∴6,9∈B,
则q=6×9=54.
∴3,9,12,15中可能有两个属于A,
∵A中的方程x2-px+27=0中,两根之和x1•x2=27,
∴3,9∈A,
∴p=3+9=12,
又∵12,15∉A,
∴12,15∉B,
∵B中的方程x2-15x+q=0中,两根之和x3+x4=15,
∴6,9∈B,
则q=6×9=54.
点评:此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
设函数f(x)是R上的偶函数,且在[0,+∞)上为增函数,则( )
| A、f(-π)>f(3)>f(-2) |
| B、f(-π)>f(-2)>f(3) |
| C、f(-π)<f(3)<f(-2) |
| D、f(-π)<f(-2)<f(3) |
已知∠B是△ABC的一个内角,下列函数能取负值的是( )
| A、sinB | ||
| B、cosB | ||
C、tan
| ||
D、cos
|
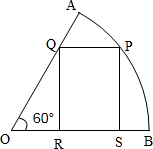 如图,已知扇形AOB的半径为1,中心角为60°,四边形PQRS是扇形的内接矩形,P为
如图,已知扇形AOB的半径为1,中心角为60°,四边形PQRS是扇形的内接矩形,P为
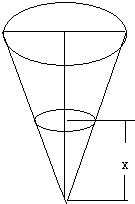 如图,圆锥型量杯口径为2R,高为h,求量杯母线上刻度V(容积)与液面深x的函数关系.
如图,圆锥型量杯口径为2R,高为h,求量杯母线上刻度V(容积)与液面深x的函数关系. 如图,扇形所含的中心角是90°,弦AB将扇形分成两个部分,各以AO为轴旋转一周所得的旋转体体积V1 与V2的比是=
如图,扇形所含的中心角是90°,弦AB将扇形分成两个部分,各以AO为轴旋转一周所得的旋转体体积V1 与V2的比是=