题目内容
11.不等式$\frac{4}{x-2}>x-2$的解集是( )| A. | (-∞,0)∪(2,4) | B. | [0,2)∪[4,+∞) | C. | [2,4) | D. | (-∞,-2]∪(4,+∞) |
分析 原不等式等价于等价于 $\frac{{x}^{2}-4x}{x-2}$<0,用穿根法求得它的解集.
解答  解:不等式$\frac{4}{x-2}>x-2$,等价于 $\frac{{x}^{2}-4x}{x-2}$<0,
解:不等式$\frac{4}{x-2}>x-2$,等价于 $\frac{{x}^{2}-4x}{x-2}$<0,
用穿根法求得它的解集为{x|x<0或2<x<4},
故选:A.
点评 本题主要考查用穿根法解分式不等式,体现了转化、数形结合的数学思想,属于基础题.

练习册系列答案
相关题目
6.设F1,F2是双曲线$\frac{x^2}{8}-{y^2}$=1的两个焦点,点P在双曲线上,且∠F1PF2=90°,则点P到x轴的距离为( )
| A. | $\sqrt{7}$ | B. | 3 | C. | $\frac{1}{3}$ | D. | $\frac{{\sqrt{7}}}{7}$ |
1.已知集合∁RM={x|lnx<e},$N=\{y|y=\frac{1}{x}(x>0)\}$,则M∩N=( )
| A. | (0,e) | B. | [e,ee) | C. | [ee,+∞) | D. | (e,+∞) |
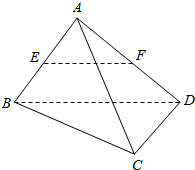 在空间四边形ABCD中,E,F分别是AB,AD的中点
在空间四边形ABCD中,E,F分别是AB,AD的中点