题目内容
12.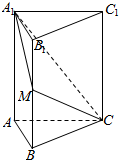 如图,在直三棱柱ABC-A1B1C1中,底面△ABC为等腰直角三角形,∠ABC=90°,AB=4,AA1=6,点M时BB1中点.
如图,在直三棱柱ABC-A1B1C1中,底面△ABC为等腰直角三角形,∠ABC=90°,AB=4,AA1=6,点M时BB1中点.(1)求证;平面A1MC⊥平面AA1C1C;
(2)求点A到平面A1MC的距离.
分析 (1)以B为原点,BC为x轴,BA为y轴,BB1为z轴,建立空间直角坐标系,利用向量法能证明平面A1MC⊥平面AA1C1C.
(2)由$\overrightarrow{A{A}_{1}}$=(0,0,6),平面A1MC的法向量$\overrightarrow{n}$=(3,-3,4),利用向量法能求出点A到平面A1MC的距离.
解答  证明:(1)以B为原点,BC为x轴,BA为y轴,BB1为z轴,建立空间直角坐标系,
证明:(1)以B为原点,BC为x轴,BA为y轴,BB1为z轴,建立空间直角坐标系,
由题意A1(0,4,6),M(0,0,3),C(4,0,0),A(0,4,0),
$\overrightarrow{M{A}_{1}}$=(0,4,3),$\overrightarrow{MC}$=(4,0,-3),$\overrightarrow{A{A}_{1}}$=(0,0,6),$\overrightarrow{AC}$=(4,-4,0),
设平面A1MC的法向量为$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{M{A}_{1}}=4y+3z=0}\\{\overrightarrow{n}•\overrightarrow{MC}=4x-3z=0}\end{array}\right.$,取x=3,得$\overrightarrow{n}$=(3,-3,4),
设平面AA1C1C的法向量$\overrightarrow{m}$=(a,b,c),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{A{A}_{1}}=6c=0}\\{\overrightarrow{m}•\overrightarrow{AC}=4a-4b=0}\end{array}\right.$,取a=1,得$\overrightarrow{m}$=(1,1,0),
∴$\overrightarrow{m}•\overrightarrow{n}$=0,
∴平面A1MC⊥平面AA1C1C.
解:(2)∵$\overrightarrow{A{A}_{1}}$=(0,0,6),平面A1MC的法向量$\overrightarrow{n}$=(3,-3,4),
∴点A到平面A1MC的距离:
d=$\frac{|\overrightarrow{A{A}_{1}}•\overrightarrow{n}|}{|\overrightarrow{n}|}$=$\frac{24}{\sqrt{34}}$=$\frac{12\sqrt{34}}{17}$.
点评 本题考查面面垂直的证明,考查点到平面的距离的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

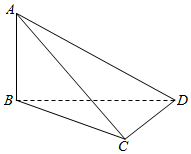 如图,在四面体ABCD中,AB⊥BD,CD⊥DB,若AB与CD所成的角的大小为60°,则二面角C-BD-A的大小为( )
如图,在四面体ABCD中,AB⊥BD,CD⊥DB,若AB与CD所成的角的大小为60°,则二面角C-BD-A的大小为( )| A. | 60°或90° | B. | 60° | C. | 60°或120° | D. | 30°或150° |
 如图,四棱锥P-ABCD,底面ABCD是边长为2的菱形,∠ABC=60°,M为侧棱PD的三等分点(靠近D点),O为AC,BD的交点,且PO⊥面ABCD,PO=$\sqrt{6}$.
如图,四棱锥P-ABCD,底面ABCD是边长为2的菱形,∠ABC=60°,M为侧棱PD的三等分点(靠近D点),O为AC,BD的交点,且PO⊥面ABCD,PO=$\sqrt{6}$.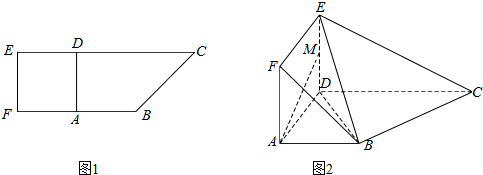
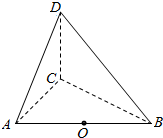 如图所示,三棱锥D-ABC中,AC,BC,CD两两垂直,AC=CD=1,$BC=\sqrt{3}$,点O为AB中点.
如图所示,三棱锥D-ABC中,AC,BC,CD两两垂直,AC=CD=1,$BC=\sqrt{3}$,点O为AB中点.