题目内容
4.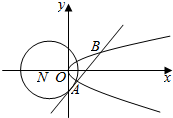 已知圆N:(x+2)2+y2=8和抛物线C:y2=2x,圆N的切线l与抛物线C交于不同的两点A,B.
已知圆N:(x+2)2+y2=8和抛物线C:y2=2x,圆N的切线l与抛物线C交于不同的两点A,B.(1)当切线l的斜率为1时.求线段AB的长;
(2)设点M(0,-2),当切线l的斜率为-1时,求证:MA⊥MB.
分析 (1)圆N的圆心N为(-2,0),半径r=2$\sqrt{2}$,设A(x1,y1),B(x2,y2),设l的方程,利用直线l是圆N的切线,求得m的值,从而可得直线l的方程,与抛物线方程联立,利用韦达定理,即可计算弦长|AB|;
(2)先求出直线l的方程,再代入抛物线方程,消去x得y2+2y-4=0.证明$\overrightarrow{MA}•\overrightarrow{MB}$=0即可.
解答 解:因为圆N:(x+2)2+y2=8,所以圆心N为(-2,0),半径r=2$\sqrt{2}$,…(1分)
设A(x1,y1),B(x2,y2),
(1)当直线l的斜率为1时,设l的方程为y=x+m即x-y+m=0
因为直线l是圆N的切线,所以$\frac{|-2+m|}{\sqrt{2}}$=2$\sqrt{2}$,解得m=-2或m=6(舍),此时直线l的方程为y=x-2,…(3分)
由$\left\{\begin{array}{l}{y=x-2}\\{{y}^{2}=2x}\end{array}\right.$消去x得y2-2y-4=0,
所以△>0,y1+y2=2,y1y2=-4,…(4分)
所以弦长|AB|=$\sqrt{1+1}$•$\sqrt{4+16}$=2$\sqrt{10}$…(6分)
(2)当直线l的斜率为-1时,设l的方程为y=-x+b即x+y-b=0
因为直线l是圆N的切线,所以$\frac{|-2-b|}{\sqrt{2}}$=2$\sqrt{2}$,解得b=2或b=-6(舍),此时直线l的方程为y=-x+2
代入抛物线方程,消去x得y2+2y-4=0,
所以△>0,y1+y2=-2,y1y2=-4,…(9分)
所以$\overrightarrow{MA}•\overrightarrow{MB}$=(x1,y1+2)•(x2,y2+2)=2y1y2+8=0,
所以MA⊥MB.…(12分)
点评 本题考查直线与抛物线的位置关系,考查弦长的计算,考查韦达定理的运用,解题的关键是联立方程,正确运用韦达定理.

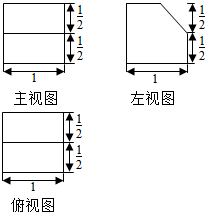
| A. | $\frac{7}{8}$ cm3 | B. | $\frac{2}{3}$ cm3 | C. | $\frac{5}{6}$ cm3 | D. | $\frac{1}{2}$ cm3 |

| A. | 20+2π | B. | 20+3π | C. | 24+2π | D. | 24+3π |
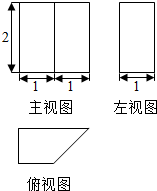
| A. | 3 | B. | $2\sqrt{2}$ | C. | $\sqrt{2}$ | D. | 1 |
| A. | 2x-y-3=0 | B. | 2x+y-3=0 | C. | x-2y-3=0 | D. | x+2y-3=0 |

| A. | 4π | B. | 12π | C. | 16π | D. | 48π |
| A. | $\frac{{2\sqrt{5}}}{7}$ | B. | $\frac{{\sqrt{35}}}{14}$ | C. | $-\frac{{2\sqrt{5}}}{7}$ | D. | $-\frac{{\sqrt{35}}}{14}$ |