题目内容
14.若某多面体的三视图(单位:cm)如图所示,则此多面体的体积是( )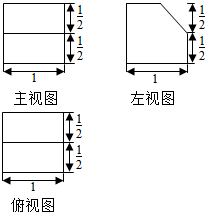
| A. | $\frac{7}{8}$ cm3 | B. | $\frac{2}{3}$ cm3 | C. | $\frac{5}{6}$ cm3 | D. | $\frac{1}{2}$ cm3 |
分析 作出几何体的直观图,可发现几何体为正方体切去一个三棱柱得到的.使用作差法求出几何体体积.
解答  解:由三视图可知该几何体为正方体去掉一个三棱柱得到的几何体.
解:由三视图可知该几何体为正方体去掉一个三棱柱得到的几何体.
正方体的边长为1,去掉的三棱柱底面为等腰直角三角形,直角边为$\frac{1}{2}$,
棱柱的高为1,棱柱的体积为$\frac{1}{2}×\frac{1}{2}×\frac{1}{2}×1$=$\frac{1}{8}$.
∴剩余几何体的体积为13-$\frac{1}{8}$=$\frac{7}{8}$.
故选A.
点评 本题考查了常见几何体的三视图和结构特征,属于基础题.

练习册系列答案
相关题目
4.某几何体的三视图如图,则该几何体的表面积为( )
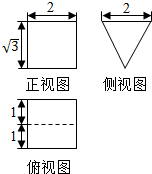

| A. | $12+\sqrt{3}$ | B. | $12+2\sqrt{3}$ | C. | $4+3\sqrt{3}$ | D. | $4+2\sqrt{3}$ |
9.已知两条直线l1:x+(1+m)y+m-2=0,l2:3mx+6y+24=0互相平行,则m的值为( )
| A. | -2或1 | B. | 2或-1 | C. | -2 | D. | 1 |
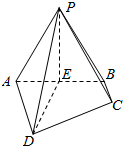 如图,在四棱锥P-ABCD中,AD∥BC,AD⊥平面PAB,△PAB是正三角形,AD=AB=2,BC=1,E是线段AB的中点
如图,在四棱锥P-ABCD中,AD∥BC,AD⊥平面PAB,△PAB是正三角形,AD=AB=2,BC=1,E是线段AB的中点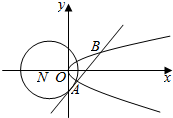 已知圆N:(x+2)2+y2=8和抛物线C:y2=2x,圆N的切线l与抛物线C交于不同的两点A,B.
已知圆N:(x+2)2+y2=8和抛物线C:y2=2x,圆N的切线l与抛物线C交于不同的两点A,B.