题目内容
4..已知f(x)=x2-2mx+2,(1)如果对一切x∈R,f(x)>0恒成立,求实数m的取值范围;
(2)当x∈[-1,+∞)时,f(x)≥m恒成立,求实数m的取值范围.
分析 (1)根据二次函数的性质求出m的范围即可;(2)设F(x)=x2-2mx+2-m,通过讨论m的范围结合二次函数的性质得到关于m的不等式组,解出即可.
解答 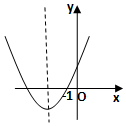 解:(1)f(x)=x2-2mx+2,
解:(1)f(x)=x2-2mx+2,
如果对一切x∈R,f(x)>0恒成立,
则△=4m2-8<0,解得,-$\sqrt{2}$<m<$\sqrt{2}$;
(2)设F(x)=x2-2mx+2-m,则当x∈[-1,+∞)时,F(x)≥0恒成立
当△=4(m-1)(m+2)<0即-2<m<1时,F(x)>0显然成立;
当△≥0时,如图所示:
F(x)≥0恒成立的充要条件为:$\left\{\begin{array}{l}△≥0\\ F(-1)≥0\\-\frac{-2m}{2}≤-1\end{array}\right.$,解得-3≤m≤-2.
综上可得实数m的取值范围为[-3,1).
点评 本题考查了函数恒成立问题,考查二次函数的性质以及分类讨论思想,是一道中档题.

练习册系列答案
相关题目
14.已知数列{an}是等比数列,a1=1,a4=8,则公比q等于( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
12.定义平面上两条相交直线的夹角为:两条相交直线交成的不超过90°的正角.已知双曲线E:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0),当其离心率$e∈[\sqrt{2},2]$时,对应双曲线的渐近线的夹角的取值范围为( )
| A. | $[0,\frac{π}{6}]$ | B. | $[\frac{π}{6},\frac{π}{3}]$ | C. | $[\frac{π}{4},\frac{π}{3}]$ | D. | $[\frac{π}{3},\frac{π}{2}]$ |
5.F1,F2是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,过点F1(作斜率为k的直线交双曲线右支于点P,且∠F1PF2为锐角,M为线段F1P的中点,过坐标原点O作OT⊥F1P于点T,且|OM|-|TM|=b-a,则k=( )
| A. | $\frac{b}{a}$ | B. | $\frac{a}{b}$ | C. | $\frac{a}{\sqrt{{a}^{2}+{b}^{2}}}$ | D. | $\frac{b}{\sqrt{{a}^{2}+{b}^{2}}}$ |
6.“所有9的倍数的数都是3的倍数,5不是9的倍数,故5不是3的倍数.”上述推理( )
| A. | 不是三段论推理,且结论不正确 | B. | 不是三段论推理,但结论正确 | ||
| C. | 是三段论推理,但小前提错 | D. | 是三段论推理,但大前提错 |



