题目内容
若复数z=cosθ+isinθ(0≤θ≤π),ω=-1+i,则|z-ω|的最大值= .
考点:复数求模
专题:计算题,数系的扩充和复数
分析:利用复数的减法代入后整理,然后运用求模公式写出|z-ω|的模,最后利用三角函数的化简进行求值.
解答:
解:由z=cosθ+isinθ,θ∈[0,π],ω=-1+i,得:z-ω=cosθ+isinθ-(-1+i)=(cosθ+1)+(sinθ-1)i,
所以|z-ω|=
=
=
,
因为θ∈[0,π],所以θ+
∈[
,
],所以cos(θ+
)∈[-
,
],
所以|z-ω|的最大值是
.
故答案为:
.
所以|z-ω|=
| (cosθ+1)2+(sinθ-1)2 |
| 3+2(cosθ-sinθ) |
3+2
|
因为θ∈[0,π],所以θ+
| π |
| 4 |
| π |
| 4 |
| 5π |
| 4 |
| π |
| 4 |
| ||
| 2 |
| ||
| 2 |
所以|z-ω|的最大值是
| 5 |
故答案为:
| 5 |
点评:本题考查了复数的模,考查了三角函数的化简与求值,考查了学生的运算求解能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知i为虚数单位,复数z=
,则复数
在复平面上的对应点位于( )
| 1+2i |
| 1-i |
. |
| z |
| A、第四象限 | B、第三象限 |
| C、第二象限 | D、第一象限 |

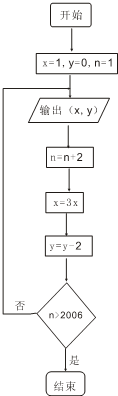 已知某算法的流程图如图示,若将输出的(x,y)依次记为(x1,y1),(x2,y2),…,(xn,yn),…
已知某算法的流程图如图示,若将输出的(x,y)依次记为(x1,y1),(x2,y2),…,(xn,yn),…