题目内容
19.已知f(x)=x2-ax+4.(1)若f(x)≥0在[$\frac{1}{2}$,4]上恒成立,求a的取值范围;
(2)若方程f(x)=3在[$\frac{1}{2}$,4]上有两个解,求a的取值范围.
分析 (1)由f(x)≥0在[$\frac{1}{2}$,4]上恒成立,得到a≤x+$\frac{4}{x}$在[$\frac{1}{2}$,4]上恒成立,利用基本不等式求出右边的最小值,即可求a的取值范围;
(2)f(x)=3,a=x+$\frac{1}{x}$,结合基本不等式,利用方程f(x)=3在[$\frac{1}{2}$,4]上有两个解,求a的取值范围.
解答 解:(1)由f(x)≥0在[$\frac{1}{2}$,4]上恒成立,得到a≤x+$\frac{4}{x}$在[$\frac{1}{2}$,4]上恒成立,
∵x+$\frac{4}{x}$≥4,当且仅当x=2时取等号,
∴a≤4;
(2)f(x)=3,∴a=x+$\frac{1}{x}$,
由g(x)=x+$\frac{1}{x}$,在[$\frac{1}{2}$,1)上单调递减,(1,4]上单调递增,g($\frac{1}{2}$)=$\frac{5}{2}$,g(4)=$\frac{17}{4}$,g(1)=2,$\frac{17}{4}>\frac{5}{2}$,
∴方程f(x)=3在[$\frac{1}{2}$,4]上有两个解,a的取值范围是(2,$\frac{5}{2}$].
点评 本题考查恒成立问题,考查基本不等式的运用,正确转化是关键.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
9.椭圆$\frac{x^2}{16}$+$\frac{y^2}{25}$=1的离心率为( )
| A. | $\frac{4}{5}$ | B. | $\frac{5}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{5}{3}$ |
10.已知命题p:函数y=ln(x2+3)+$\frac{1}{{ln({x^2}+3)}}$的最小值是2;命题q:x>2是x>l的充分不必要条件.则下列命题为真命题的是( )
| A. | p∧q | B. | ?p∧?q | C. | ?p∧q | D. | p∧?q |
9.随机变量ξ的分布列如表,则D(ξ)=$\frac{5}{9}$
| ξ | 0 | 1 | 2 |
| P | $\frac{1}{2}$ | $\frac{1}{3}$ | p |
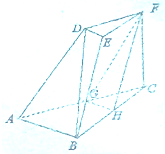 如图,三棱台DEF-ABC中,AB=2DE,G,H分别为AC,BC的中点.
如图,三棱台DEF-ABC中,AB=2DE,G,H分别为AC,BC的中点.