经过点A(3.0).垂直于极轴的直线的极坐标方程是ρcosθ=3．题目和参考答案——青夏教育精英家教网—

题目内容

18．经过点A（3，0）、垂直于极轴的直线的极坐标方程是ρcosθ=3．

分析设直线上的任意一点P（ρ，θ）．PA⊥x轴，在Rt△OAP中，利用边角关系即可得出．

解答解：如图所示，设直线上的任意一点P（ρ，θ）．
PA⊥x轴，在Rt△OAP中，ρcosθ=3．
∴满足条件的直线方程为：ρcosθ=3．
故答案为：ρcosθ=3．

点评本题考查了直线的极坐标方程、直角三角形的边角关系，考查了计算能力，属于基础题．

练习册系列答案

提分百分百检测卷单元期末测试卷系列答案

9．椭圆$\frac{x^2}{16}$+$\frac{y^2}{25}$=1的离心率为（　　）

6．已知二阶矩阵$M=[{\begin{array}{l}a&1\\ 1&b\end{array}}]$属于特征值λ=5的一个特征向量为$\overrightarrow{e}$=$[\begin{array}{l}{1}\\{1}\end{array}]$，则a+b=8．

13．已知圆C与直线y=-x+2$\sqrt{2}$相切，圆心在x轴上，且该圆被直线y=x截得的弦长为4$\sqrt{2}$．
（1）求圆C的方程；
（2）过点N（-1，0）作斜率为k（k≠0）的直线l与圆C交于A，B两点．若直线OA与OB的斜率之积为-（3+$\sqrt{2}$）k²，求$\overrightarrow{OA}$•$\overrightarrow{OB}$的值．

3．给定集合A、B，定义：A*B={x|x∈B或x∈A，但x∉A∩B}，又已知A={0，1，2}，B={1，2，3}，则A*B=（　　）

10．已知命题p：函数y=ln（x²+3）+$\frac{1}{{ln（{x^2}+3）}}$的最小值是2；命题q：x＞2是x＞l的充分不必要条件．则下列命题为真命题的是（　　）

7．已知函数f（x）=$\frac{ax-1}{{e}^{x}}$
（1）当a=1时，求函数f（x）的最值；
（2）若对任意的x∈（$\frac{1}{2}$，1），f（x）＞x恒成立，求实数a的取值范围．

8．

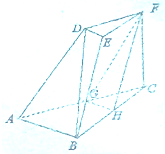如图，三棱台DEF-ABC中，AB=2DE，G，H分别为AC，BC的中点．
（Ⅰ）求证：BD∥平面FGH．
（Ⅱ）若CF⊥BC，AB⊥BC，求证：BCD⊥EGH．

试题分类