题目内容

10．函数y=sin2x-2sin2x+1的最大值为（　　）
A．2B．$\sqrt{2}$C．3D．$\sqrt{3}$

分析 使用二倍角公式和两角和的正弦公式化简，根据正弦函数的性质得出最大值．

解答 解：y=sin2x+cos2x=$\sqrt{2}$sin（2x+$\frac{π}{4}$）．
∴y的最大值是$\sqrt{2}$．
故选：B．

点评 本题考查了三角函数的恒等变换，正弦函数的图象与性质，属于基础题．

练习册系列答案
相关题目
20．方程$\frac{|x|}{3}$+$\frac{|y|}{4}$=1所表示的图形在直角坐标系中所围成的面积为24．
1．设函数f（x）=$\frac{1}{cosx}$+$\frac{a}{sinx}$，若对任意x∈（0，$\frac{π}{2}$），不等式f（x）≥8恒成立，则实数a的取值范围是[3$\sqrt{3}$，+∞）．
18．在△ABC中，已知a=18，B=60°，C=75°，求b的值．
5．在△ABC中，a、b、c分别是角A、B、C所对的边，1+$\frac{tanC}{tanB}$=$\frac{2a}{b}$．
（]）求角C的大小；
（2）若cos（B+$\frac{π}{6}$）=$\frac{1}{3}$，求sinA的值；
（3）若（a+b）2-c2=4，求3a+b的最小值．
15．下列函数中是偶函数的为（　　）
A．f（x）=|x-1|B．f（x）=cos（x-$\frac{π}{2}$）C．f（x）=0D．f（x）=1+x2（x≥0）
2．已知$\overrightarrow{a}$=（1，$\sqrt{3}$），$\overrightarrow{b}$=（-$\sqrt{3}$，-1），则＜$\overrightarrow{a}$，$\overrightarrow{b}$＞=$\frac{2π}{3}$．
19．向量$\overrightarrow{a}$、$\overrightarrow{b}$的坐标分别是（2，-3），（5，-4），求$\overrightarrow{a}$•$\overrightarrow{b}$．
17．某空间几何体的三视图如图所示，则该几何体的体积为（　　）
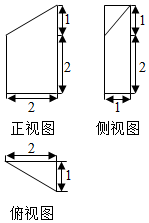
A．$\frac{8}{9}$B．$\frac{8}{3}$C．3D．$\frac{17}{3}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网