题目内容
5.(1)求一个焦点为(13,0),且离心率为$\frac{13}{5}$的双曲线的标准方程;(2)已知抛物线的焦点在x轴上,抛物线上的点 M(-3,m)到焦点的距离等于5,求抛物线的标准方程和m的值.
分析 (1)由题意可知双曲线的焦点在x轴上,再由已知求得c、a的值,结合隐含条件求得b,则椭圆方程可求;
(2)由题意设抛物线方程为y2=-2px(p>0),再由抛物线焦半径公式求得p,得到抛物线方程,把M的坐标代入抛物线方程求得m值.
解答 解:(1)依题意可知,双曲线的焦点在x轴上,且c=13,
又$\frac{c}{a}=\frac{13}{5}$,∴a=5,$b=\sqrt{{c^2}-{a^2}}=12$,
故其标准方程为$\frac{x^2}{25}-\frac{y^2}{144}=1$;
(2)设抛物线方程为y2=-2px(p>0),则焦点F($-\frac{p}{2}$,0),准线方程为$x=\frac{p}{2}$,
根据抛物线的定义,点M到焦点的距离等于5,也就是M到准线的距离为5,则$3+\frac{p}{2}=5$,∴p=4,
因此,抛物线方程为y2=-8x,
又点 M(-3,m)在抛物线上,于是m2=24,∴$m=±2\sqrt{6}$.
点评 本题考查双曲线及抛物线标准方程的求法,考查利用抛物线定义求标准方程,体现了数学转化思想方法,是基础题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
13.命题:“?x0∈R,x02+1>0或x0>sinx0”的否定是( )
| A. | ?x∈R,x2+1≤0且x≤sinx | B. | ?x∈R,x2+1≤0或x≤sinx | ||
| C. | ?x0∈R,x${\;}_{0}^{2}$+1≤0且x0>sinx0 | D. | ?x0∈R,x${\;}_{0}^{2}$+1≤0或x0≤sinx0 |
17.某空间几何体的三视图如图所示,则该几何体的体积为( )
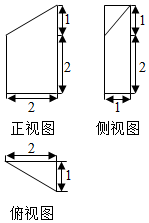

| A. | $\frac{8}{9}$ | B. | $\frac{8}{3}$ | C. | 3 | D. | $\frac{17}{3}$ |
