题目内容
7.直线3x+4y+12=0与⊙C:(x-1)2+(y-1)2=9的位置关系是相离.分析 由已知中直线与圆的方程,求出圆心到直线的距离,进而可得答案.
解答 解:⊙C:(x-1)2+(y-1)2=9的圆心坐标为(1,1),半径r=3,
圆心到直线3x+4y+12=0的距离d=$\frac{|3+4+12|}{\sqrt{{3}^{2}+{4}^{2}}}$=$\frac{19}{5}$>3,
故直线与圆相离,
故答案为:相离
点评 本题考查的知识点是直线与圆的位置关系难度不大,熟练掌握点到直线之间距离公式,是解答的关键.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
17.某空间几何体的三视图如图所示,则该几何体的体积为( )
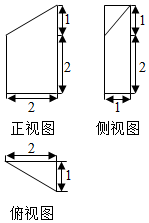

| A. | $\frac{8}{9}$ | B. | $\frac{8}{3}$ | C. | 3 | D. | $\frac{17}{3}$ |
18.已知函数f(x)=x2-2ax+5(a>1),g(x)=log3x.若函数f(x)的定义域与值域均为[1,a],且对于任意的x1,x2∈[1,a+1],$|{f({x_1})-g({x_2})}|≤{4^t}+{2^t}$恒成立,则满足条件的实数t的取值范围是( )
| A. | [-2,8] | B. | [0,8] | C. | [0,+∞) | D. | [0,8) |
19.“α=$\frac{π}{2}$”是sin(α-β)=cosβ“的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
