题目内容
已知抛物线 :
: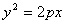
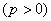 ,直线交此抛物线于不同的两个点
,直线交此抛物线于不同的两个点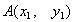 、
、 .
.
(1)当直线过点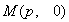 时,证明
时,证明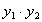 为定值;
为定值;
(2)如果直线过点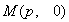 ,过点
,过点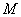 再作一条与直线垂直的直线
再作一条与直线垂直的直线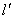 交抛物线
交抛物线 于两个不同点
于两个不同点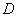 、
、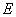 .设线段
.设线段 的中点为
的中点为 ,线段
,线段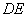 的中点为
的中点为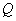 ,记线段
,记线段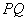 的中点为
的中点为 .问是否存在一条直线和一个定点,使得点
.问是否存在一条直线和一个定点,使得点 到它们的距离相等?若存在,求出这条直线和这个定点;若不存在,请说明理由.
到它们的距离相等?若存在,求出这条直线和这个定点;若不存在,请说明理由.
解:(1)过点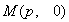 与抛物线有两个交点,设
与抛物线有两个交点,设 ,由
,由 得
得 ,
,
 .
.
(2)依题意直线的斜率存在且不为零,由(1)得点 的纵坐标为
的纵坐标为 ,代入
,代入 得
得 ,即
,即 .
.
由于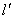 与互相垂直,将点
与互相垂直,将点 中的
中的 用
用 代,得
代,得 .
.
设 ,则
,则 消
消 得
得
由抛物线的定义知存在直线 ,点
,点 ,点
,点 到它们的距离相等.
到它们的距离相等.

练习册系列答案
相关题目
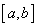 的函数
的函数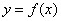 图象的两个端点为
图象的两个端点为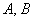 ,向量
,向量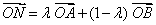 ,
, 是
是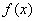 图象上任意一点,其中
图象上任意一点,其中 .若不等式
.若不等式 恒成立,则称函数
恒成立,则称函数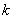 范围线性近似”,其中最小的正实数
范围线性近似”,其中最小的正实数 上函数中,线性近似阀值最小的是( )
上函数中,线性近似阀值最小的是( ) B.
B. C.
C.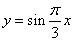 D.
D.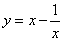
 .
. 与直线
与直线 相交,若在
相交,若在 轴右侧的交点自左向右依次记为
轴右侧的交点自左向右依次记为 ,
, ,
, ,……,则
,……,则 等于( )
等于( )







 ,元素
,元素
 的代数余子式为
的代数余子式为 ,
, , 函数
, 函数 的定义域为
的定义域为 若
若 求实数
求实数 的取值范围.
的取值范围. 中,已知
中,已知 ,则最大角等于 .
,则最大角等于 . 的通项公式为
的通项公式为 ,下列四个命题:
,下列四个命题: :数列
:数列 :数列
:数列 是递增数列;
是递增数列; :数列
:数列 是递增数列;
是递增数列; :数列
:数列 是递增数列.其中真命题的是 .
是递增数列.其中真命题的是 . 是母线
是母线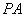 的中点,
的中点,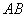 是底面圆的直径,底面半径
是底面圆的直径,底面半径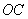 与母线
与母线 所成的角的大小等于
所成的角的大小等于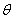 .
.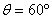 时,求异面直线
时,求异面直线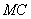 与
与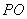 所成的角;
所成的角;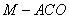 的体积最大时,求
的体积最大时,求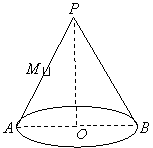
 的焦点与双曲线
的焦点与双曲线 的右焦点重合,则
的右焦点重合,则 _________.
_________.