题目内容
1．已知f（x）是定义在R上的奇函数，且当x＞0时，f（x）=$\left\{\begin{array}{l}{sin\frac{πx}{3}，0＜x≤4}\\{lo{g}_{4}x，x＞4}\end{array}\right.$，f（f（-16））=（ ）| A． | -$\frac{1}{2}$ | B． | -$\frac{\sqrt{3}}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{\sqrt{3}}{2}$ |
分析 根据函数的奇偶性求出f（-16）的值是-2，再求出f（-2）的值即可．
解答 解：∵f（-16）=-f（16）=-${log}_{4}^{16}$=-2，
∴f（f（-16））=f（-2）=-f（2）=-sin$\frac{2π}{3}$=-sin$\frac{π}{3}$=-$\frac{\sqrt{3}}{2}$，
故选：B．
点评 本题考查了函数的奇偶性的性质，求函数值问题，是一道基础题．
练习册系列答案
相关题目
函数f（x）=Asin（ωx+φ）（A＞0，ω＞0）的部分图象如图所示，则f（0）=$\frac{{\sqrt{6}}}{2}$．
9．已知函数$f（x）=asinx-\sqrt{3}cosx$关于直线$x=-\frac{π}{6}$对称，且f（x1）•f（x2）=-4，则|x1+x2|的最小值为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{5π}{6}$ | D． | $\frac{2π}{3}$ |
6．已知全集U={-2，0，1，2}，集合A={x|x2+x-2=0}，则∁UA=（ ）
| A． | {-2，1} | B． | {-2，0} | C． | {0，2} | D． | {0，1} |
13．
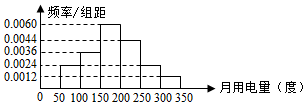为了了解长沙市居民月用电情况，抽查了该市100户居民用电量（单位：度），得到频率分布直方图如下：根据如图可得到这100户居民月用电量在[150，300]的用户数是（ ）
为了了解长沙市居民月用电情况，抽查了该市100户居民用电量（单位：度），得到频率分布直方图如下：根据如图可得到这100户居民月用电量在[150，300]的用户数是（ ）| A． | 70 | B． | 64 | C． | 48 | D． | 30 |
1．已知集合P={x|x2-2x-3≥0}，Q={x|1＜x＜4}，则P∩Q=（ ）
| A． | {x|-1＜x＜3} | B． | {x|3≤x＜4} | C． | {x|x≥4或x＜-3} | D． | {x|x＜-1或x＞3} |