题目内容
3.双曲线$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{k}$=1的实轴长为8,离心率e∈(1,2),则k的取值范围是( )| A. | (-∞,0) | B. | (-48,0) | C. | (-192,0) | D. | (-60,-48) |
分析 利用双曲线$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{k}$=1的实轴长为8,离心率e∈(1,2),可得$\sqrt{\frac{16-k}{16}}$∈(1,2),即可求出k的取值范围.
解答 解:∵双曲线$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{k}$=1的实轴长为8,离心率e∈(1,2),
∴$\sqrt{\frac{16-k}{16}}$∈(1,2),
∴-48<k<0,
故选B.
点评 本题考查双曲线的方程与性质,考查学生的计算能力,属于中档题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
10.经过点$({\frac{1}{2},\frac{{\sqrt{3}}}{2}})$的圆x2+y2=1的切线方程是( )
| A. | $x+\sqrt{3}y=2$ | B. | $\sqrt{3}x+y=2$ | C. | $x+\sqrt{3}y=1$ | D. | $\sqrt{3}x+y=1$ |
18.直线2x-y-4=0与抛物线y2=6x交于A、B两点,则线段AB的长度为( )
| A. | $\frac{{\sqrt{265}}}{2}$ | B. | $\frac{{\sqrt{285}}}{2}$ | C. | $\frac{{\sqrt{305}}}{2}$ | D. | $\frac{{\sqrt{335}}}{2}$ |
12.若M{x|y=2x+1},N={y|y=-x2},则集合M,N的关系是( )
| A. | M∩N={(-1,1)} | B. | M∩N=∅ | C. | M⊆N | D. | N⊆M |
13.已知F1、F2是双曲线E:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,点M在E的渐近线上,且MF1与x轴垂直,sin∠MF2F1=$\frac{1}{3}$,则E的离心率为( )
| A. | $\frac{\sqrt{6}}{2}$ | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | 2 |
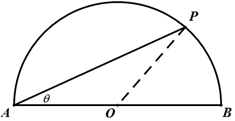 运动员小王在一个如图所示的半圆形水域(O为圆心,AB是半圆的直径)进行体育训练,小王先从点A出发,沿着线段AP游泳至半圆上某点P处,再从点P沿着弧PB跑步至点B处,最后沿着线段BA骑自行车回到点A处,本次训练结束.已知OA=1500m,小王游泳、跑步、骑自行车的平均速度分别为2m/s,4m/s,10m/s,设∠PAO=θrad.
运动员小王在一个如图所示的半圆形水域(O为圆心,AB是半圆的直径)进行体育训练,小王先从点A出发,沿着线段AP游泳至半圆上某点P处,再从点P沿着弧PB跑步至点B处,最后沿着线段BA骑自行车回到点A处,本次训练结束.已知OA=1500m,小王游泳、跑步、骑自行车的平均速度分别为2m/s,4m/s,10m/s,设∠PAO=θrad.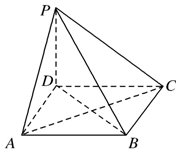 如图,在四棱锥 P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=$\sqrt{2}$a.
如图,在四棱锥 P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=$\sqrt{2}$a.