题目内容
10.在平面直角坐标系中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,已知直线l的极坐标方程为:ρsinθ+ρcosθ=2,曲线C的极坐标方程为:ρcos2θ=asinθ(a>0),曲线C与直线l的交点为M,N.(Ⅰ)当a=1时,求直线l和曲线C相交的弦长|MN|;
(Ⅱ)若$\overrightarrow{OM}$•$\overrightarrow{ON}$=0,求△OMN的面积.
分析 (Ⅰ)化极坐标方程为普通方程,当a=1时,直接求直线l和曲线C的解得坐标,然后求解弦长|MN|;
(Ⅱ)联立直线与抛物线方程,利用向量的数量积,求解弦长MN,清楚圆心到直线的距离即可求解三角形的面积.
解答 解:(Ⅰ)直线l的极坐标方程为:ρsinθ+ρcosθ=2,直线的普通方程为:x+y=2,
曲线C的极坐标方程为:ρcos2θ=asinθ(a>0),它的普通方程为:ay=x2.当a=1时,
:x2+x-2=0,解得x=1或x=-2,曲线C与直线l的交点为M(-2,4),N
(1,1).
∴|MN|=$\sqrt{9+9}$=3$\sqrt{2}$…(5分)
(Ⅱ)把ay=x2代入可得直线l的普通方程x+y=2消去y得
:x2+ax-2a=0,设M(x1,y1),N(x2,y2),x1+x2=-a,x1x2=-2a,则
y1y2=(-x1+2)(-x2+2)=4∴
$\overrightarrow{OM}$•$\overrightarrow{ON}$=0,∴x1x2+y1y2=-2a+4=0,解得a=2,
此时${x_1}+{x_2}=-2,{x_1}{x_2}=-4,|{x_1}-{x_2}|=\sqrt{{{({{x_1}+{x_2}})}^2}-4{x_1}{x_2}}=2\sqrt{5}$.
|MN|=$\sqrt{2}$|x1-x2|=2$\sqrt{10}$.原点到直线的距离为:h=$\frac{|2|}{\sqrt{2}}$=$\sqrt{2}$.
∴S△0MN=$\frac{1}{2}×\sqrt{2}×2\sqrt{10}$=2$\sqrt{5}$.
点评 本题考试极坐标与普通方程互化,直线与抛物线的位置关系的应用,考查计算能力.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
1.已知角α的正弦线和余弦线长度相等,且α的终边在第三象限,则tanα等于( )
| A. | 0 | B. | 1 | C. | -1 | D. | $\sqrt{3}$ |
15.若b<a<0,则下列不等式一定成立的是( )
| A. | a3<b3 | B. | ab>b2 | C. | ac2>bc2 | D. | $\frac{1}{a}$<$\frac{1}{b}$ |
2.某用水量较大的企业为积极响应政府号召的“节约用水,我们共同的责任”的倡议,对生产设备进行技术改造,下表提供了该企业节约用水技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产用水y(吨)的几组对照数据:
(1)若x,y之间是线性相关,请根据表中提供的数据,求y关于x的线性回归方程y=bx+a;
(2)已知该厂技术改造前100吨甲产品的生产用水为120吨,试根据(1)中求出的线性回归方程,预测技术改造后生产100吨甲产品的用水量比技术改造前减少了多少吨?
(参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{1}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n\stackrel{-2}{x}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$)
| x | 1 | 2 | 3 | 4 |
| y | 0.4 | 0.9 | 1.1 | 1.6 |
(2)已知该厂技术改造前100吨甲产品的生产用水为120吨,试根据(1)中求出的线性回归方程,预测技术改造后生产100吨甲产品的用水量比技术改造前减少了多少吨?
(参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{1}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n\stackrel{-2}{x}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$)
20.已知函数f(x)=ax3+bx2+cx,其导函数为f′(x)的部分值如表所示:
根据表中数据,回答下列问题:
(Ⅰ)实数c的值为6;当x=3时,f(x)取得极大值(将答案填写在横线上).
(Ⅱ)求实数a,b的值.
(Ⅲ)若f(x)在(m,m+2)上单调递减,求m的取值范围.
| x | -3 | -2 | 0 | 1 | 3 | 4 | 8 |
| f'(x) | -24 | -10 | 6 | 8 | 0 | -10 | -90 |
(Ⅰ)实数c的值为6;当x=3时,f(x)取得极大值(将答案填写在横线上).
(Ⅱ)求实数a,b的值.
(Ⅲ)若f(x)在(m,m+2)上单调递减,求m的取值范围.
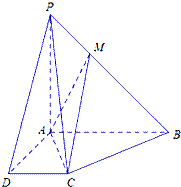 如图所示,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AB=AD=AP=2CD=2,M是棱PB上一点.
如图所示,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AB=AD=AP=2CD=2,M是棱PB上一点.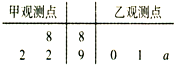 如图,茎叶图记录了某城市甲、乙两个观测点连续三天观测到的空气质量指数(AQI).乙观测点记录中有一个数字模糊无法确认,已知该数是0,1,…,9中随机的一个数,并在图中以a表示.
如图,茎叶图记录了某城市甲、乙两个观测点连续三天观测到的空气质量指数(AQI).乙观测点记录中有一个数字模糊无法确认,已知该数是0,1,…,9中随机的一个数,并在图中以a表示.