题目内容
18.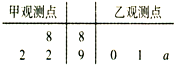 如图,茎叶图记录了某城市甲、乙两个观测点连续三天观测到的空气质量指数(AQI).乙观测点记录中有一个数字模糊无法确认,已知该数是0,1,…,9中随机的一个数,并在图中以a表示.
如图,茎叶图记录了某城市甲、乙两个观测点连续三天观测到的空气质量指数(AQI).乙观测点记录中有一个数字模糊无法确认,已知该数是0,1,…,9中随机的一个数,并在图中以a表示.(Ⅰ)若甲、乙两个观测点记录数据的平均值相同,求a的值;
(Ⅱ)当a=2时,分别从甲、乙两观测点记录的数据中各随机抽取一天的观测值,记这两观测值之差的绝对值为X,求|X|≤2的概率.
分析 (Ⅰ)直接由甲、乙两个小组的数学平均成绩相等列式求解a的值;
(Ⅱ)用枚举法列出所有可能的成绩结果,查出两名同学的数学成绩之差的绝对值不超过2分的情况数,然后由古典概率模型概率计算公式求概率.
解答 解:(Ⅰ)由甲、乙两个小组的数学平均成绩相等,
得$\frac{1}{3}$(88+92+92)=$\frac{1}{3}$[90+91+(90+a)],
解得a=1;
(Ⅱ)设“这两名同学的数学成绩之差的绝对值不超过(2分)”为事件B,
当a=2时,分别从甲、乙两组同学中各随机选取一名同学,所有可能的成绩结果有3×3=9种,它们是:
(88,90),(88,91),(88,92),(92,90),(92,91),(92,92),(92,90),
(92,91),(92,92).
∴事件B的结果有7种,它们是:(88,90),(92,90),(92,91),(92,92),(92,90),
(92,91),(92,92).
∴两名同学的数学成绩之差的绝对值不超过(2分)的概率P(B)=$\frac{7}{9}$.
点评 本题考查了茎叶图,考查了等可能事件的概率及古典概型概率计算公式,是基础的计算题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
8.复数z1,z2满足|z1|=|z2|=1,|z1+z2|=$\sqrt{2}$,则|z1-z2|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
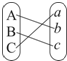 连线方式表示为$(\begin{array}{l}{A^{\;}}{B^{\;}}C\\{b^{\;}}{c^{\;}}a\end{array})$,规定第一行A,B,C的顺序固定不变,请列出所有连线的情况;
连线方式表示为$(\begin{array}{l}{A^{\;}}{B^{\;}}C\\{b^{\;}}{c^{\;}}a\end{array})$,规定第一行A,B,C的顺序固定不变,请列出所有连线的情况;