题目内容
19.已知A(0,a),B(0,b),(0<a<b),在x轴的正半轴上求点C,使∠ACB最大,并求出最大角的余弦值.分析 根据题目所给的条件,用直线和圆的位置关系,确定点的位置,由正弦定理得,当圆与X轴相切时,要求的角最大,写出角的正切值,不是特殊角,用反三角函数来表示.
解答 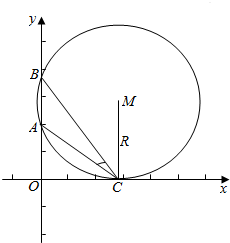 解:设点C的坐标是(x,0),在三角形ABC中,根据正弦定理知:
解:设点C的坐标是(x,0),在三角形ABC中,根据正弦定理知:
sin∠ACB=$\frac{b-a}{2R}$,其中R是三角形ABC外接圆的半径.
故当R最小时,角∠ACB最大.
在过A与B定点的圆中当且仅当C是圆与x轴相切时,半径最小,
∴切点C即为所求,由切割线定理知OC2=OA•OB=ab,
∴OC=$\sqrt{ab}$,即点C坐标为($\sqrt{ab}$,0)时,KAC=$\frac{a-0}{0-\sqrt{ab}}$=-$\frac{a}{\sqrt{ab}}$=-$\sqrt{\frac{a}{b}}$,KBC=$\frac{b-0}{0-\sqrt{ab}}$=-$\sqrt{\frac{b}{a}}$,
∠ACB可以认为是直线BC到直线AC的角,tan∠ACB=$\frac{{K}_{AC}{-K}_{BC}}{1{+K}_{AC}{•K}_{BC}}$=$\frac{b-a}{2\sqrt{ab}}$,
即∠ACB=arctan$\frac{b-a}{2\sqrt{ab}}$.
点评 认识向量的代数特性.向量的坐标表示,实现了“形”与“数”的互相转化.以向量为工具,几何问题可以代数化,代数问题可以几何化,属于中档题.

练习册系列答案
相关题目
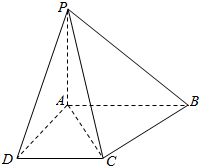 如图四棱锥P-ABCD中,PB=PC,底面ABCD是直角梯形,AB∥DC,∠ABC=60°,DC=1,AD=$\sqrt{3}$.
如图四棱锥P-ABCD中,PB=PC,底面ABCD是直角梯形,AB∥DC,∠ABC=60°,DC=1,AD=$\sqrt{3}$.