题目内容
9.己知数列{log2(an-1)}为等差数列,且a1=3,a2=5.(1)求证:数列{an-1}是等比数列;
(2)求$\frac{1}{{a}_{2}-{a}_{1}}$+$\frac{1}{{a}_{3}-{a}_{2}}$+…+$\frac{1}{{a}_{n+1}-{a}_{n}}$的值.
分析 (1)数列{log2(an-1)} 公差d=log24-log22=1,从而${log}_{2}\frac{{a}_{n}-1}{{a}_{n-1}-1}$=1,由此能证明数列{an-1}是以2为底,以2为首项的等比数列.
(2)由${a}_{n}={2}^{n}+1$,得$\frac{1}{{a}_{n+1}-{a}_{n}}$=$\frac{1}{{2}^{n+1}-{2}^{n}}$=$\frac{1}{{2}^{n}}$,由此能求出$\frac{1}{{a}_{2}-{a}_{1}}$+$\frac{1}{{a}_{3}-{a}_{2}}$+…+$\frac{1}{{a}_{n+1}-{a}_{n}}$的值.
解答 证明:(1)∵数列{log2(an-1)}为等差数列,a1=3,a2=5.
设数列{log2(an-1)} 公差为d,
∴d=log24-log22=1,
∴log2(an-1)-log2(an-1-1)=${log}_{2}\frac{{a}_{n}-1}{{a}_{n-1}-1}$=1,
∴$\frac{{a}_{n}-1}{{a}_{n-1}-1}$=2,a1-1=2,
∴数列{an-1}是以2为底,以2为首项的等比数列.
(2)∵数列{an-1}是以2为底,以2为首项的等比数列,
∴an-1=2n,∴${a}_{n}={2}^{n}+1$,
∴$\frac{1}{{a}_{n+1}-{a}_{n}}$=$\frac{1}{{2}^{n+1}-{2}^{n}}$=$\frac{1}{{2}^{n}}$,
∴$\frac{1}{{a}_{2}-{a}_{1}}$+$\frac{1}{{a}_{3}-{a}_{2}}$+…+$\frac{1}{{a}_{n+1}-{a}_{n}}$
=$\frac{1}{2}+\frac{1}{{2}^{2}}+…+\frac{1}{{2}^{n}}$
=$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$
=1-$\frac{1}{{2}^{n}}$.
点评 本题考查等比数列的证明,考查数列的前n项和的求法,是中档题,解题时要认真审题,注意构造法的合理运用.

| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{6}$ |
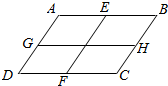 已知E,F,G,H分别是四边形ABCD四条边AB,CD,AD,BC的中点,求$\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{AD}$+$\overrightarrow{DC}$=2($\overrightarrow{EF}$+$\overrightarrow{GH}$)
已知E,F,G,H分别是四边形ABCD四条边AB,CD,AD,BC的中点,求$\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{AD}$+$\overrightarrow{DC}$=2($\overrightarrow{EF}$+$\overrightarrow{GH}$)