题目内容
10.x,y满足$\left\{\begin{array}{l}{y≥0}\\{ax+y-1≤0}\\{3x-2y-2≤0}\end{array}\right.$,若z=x2-10x+y2的最小值为-12.则实数a的取值范围是a≤-$\frac{1}{2}$.分析 由题意作平面区域,化简可得(x-5)2+y2的最小值为13,从而结合图象解得.
解答 解:由题意作平面区域如下,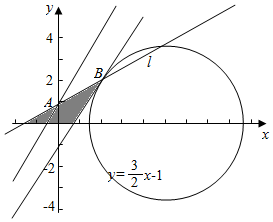 ,
,
∵z=x2-10x+y2=(x-5)2+y2-25的最小值为-12,
∴(x-5)2+y2的最小值为13,
直线ax+y-1=0恒过点A(0,1),
直线y=$\frac{3}{2}$x-1与圆(x-5)2+y2=13相切于点B(2,2);
∵ax+y-1=0可化为y=-ax+1,
故-a≥kAB=$\frac{2-1}{2-0}=\frac{1}{2}$,
故a≤-$\frac{1}{2}$;
故答案为:a≤-$\frac{1}{2}$.
点评 本题考查了线性规划的变形应用及数形结合的思想应用;关键是正确画图,利用几何意义完成;属于中档题.

练习册系列答案
相关题目
5.执行如图的程序框图,如果输入x=1,则输出t的值为( )


| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
15.已知双曲线的中心在原点,焦点在坐标轴上,一条渐近线方程为3x+4y=0,则该双曲线的离心率是( )
| A. | $\frac{5}{3}$ | B. | $\frac{5}{4}$ | C. | $\frac{4}{3}$或$\frac{5}{3}$ | D. | $\frac{5}{3}$或$\frac{5}{4}$ |
19.过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点F作渐近线的垂线,垂足为P,线段OP的垂直平分线交y轴于点Q(其中O为坐标原点),若OFP的面积是OQP的面积的6倍,则该双曲线的离心率为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | 3 | D. | $\sqrt{5}$ |
20. 执行如图的程序框图,则输出的S等于( )
执行如图的程序框图,则输出的S等于( )
 执行如图的程序框图,则输出的S等于( )
执行如图的程序框图,则输出的S等于( )| A. | 0 | B. | -3 | C. | -10 | D. | -25 |
