题目内容
1.四边形ABCD中,AC⊥BD且AC=2,BD=3,则$\overrightarrow{AB}$•$\overrightarrow{CD}$的最小值为-$\frac{13}{4}$.分析 通过建立坐标系,设C(a,0),D(0,b),利用数量积的坐标运算得出数量积关于a,b的函数,求出函数的最小值.
解答 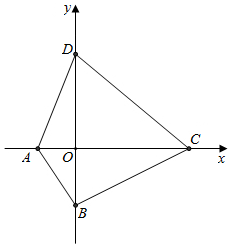 解:设AC与BD交点为O,以O为原点,AC,BD为坐标轴建立平面直角坐标系,
解:设AC与BD交点为O,以O为原点,AC,BD为坐标轴建立平面直角坐标系,
设C(a,0),D(0,b),则A(a-2,0),B(0,b-3),
∴$\overrightarrow{AB}$=(2-a,b-3),$\overrightarrow{CD}$=(-a,b).
∴$\overrightarrow{AB}•\overrightarrow{CD}$=a(a-2)+b(b-3)=(a-1)2+(b-$\frac{3}{2}$)2-$\frac{13}{4}$.
∴当a=1,b=$\frac{3}{2}$时,$\overrightarrow{AB}$•$\overrightarrow{CD}$取得最小值-$\frac{13}{4}$.
故答案为:-$\frac{13}{4}$.
点评 本题考查平面向量数量积的运算,涉及向量的坐标运算和向量的模的计算以及向量的夹角公式等基础知识,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
9.已知m,n是不重合的两条直线,α,β是不重合的两个平面,则下列命题中错误的是( )
| A. | 若m⊥α,m⊥β,则α∥β | B. | 若m?α,m⊥β,则α⊥β | C. | 若m⊥α,n∥α,则m⊥n | D. | 若m⊥α,α⊥β,则m∥β |