题目内容
19.过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点F作渐近线的垂线,垂足为P,线段OP的垂直平分线交y轴于点Q(其中O为坐标原点),若OFP的面积是OQP的面积的6倍,则该双曲线的离心率为( )| A. | $\sqrt{3}$ | B. | 2 | C. | 3 | D. | $\sqrt{5}$ |
分析 根据条件分别求出P,Q的坐标,结合三角形的面积公式建立方程进行求解即可.
解答 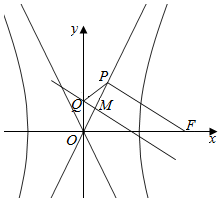 解:双曲线渐近线的方程为y=$\frac{b}{a}$x,则PF的斜率k=-$\frac{a}{b}$,
解:双曲线渐近线的方程为y=$\frac{b}{a}$x,则PF的斜率k=-$\frac{a}{b}$,
则PF的方程为y=-$\frac{a}{b}$(x-c),
由$\left\{\begin{array}{l}{y=\frac{b}{a}x}\\{y=-\frac{a}{b}(x-c)}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{{a}^{2}}{c}}\\{y=\frac{ab}{c}}\end{array}\right.$,即P($\frac{{a}^{2}}{c}$,$\frac{ab}{c}$),
OP的中点M($\frac{{a}^{2}}{2c}$,$\frac{ab}{2c}$),
OP的中垂线的方程为y-$\frac{ab}{2c}$=-$\frac{a}{b}$(x-$\frac{{a}^{2}}{2c}$),
令x=0,则y=$\frac{ab}{2c}$+$\frac{a}{b}$•$\frac{{a}^{2}}{2c}$=$\frac{ac}{2b}$,即Q(0,$\frac{ac}{2b}$),
则OQP的面积S=$\frac{1}{2}$•$\frac{ac}{2b}$•$\frac{{a}^{2}}{c}$=$\frac{{a}^{3}}{4b}$,
则OFP的面积S=$\frac{1}{2}$•c•$\frac{ab}{c}$=$\frac{ab}{2}$,
∵OFP的面积是OQP的面积的6倍,
∴6×$\frac{{a}^{3}}{4b}$=$\frac{ab}{2}$,
即b2=3a2,
则b2=3a2=c2-a2,
即4a2=c2,
则c=2a,
即离心率e=$\frac{c}{a}$=2,
故选:B.
点评 本题主要考查双曲线的性质的应用,根据双曲线渐近线之间的关系求出交点坐标,结合三角形的面积公式是解决本题的关键.考查学生的计算能力.

| A. | 若m⊥α,m⊥β,则α∥β | B. | 若m?α,m⊥β,则α⊥β | C. | 若m⊥α,n∥α,则m⊥n | D. | 若m⊥α,α⊥β,则m∥β |
| A. | $\frac{4}{{π}^{2}}$ | B. | $\frac{2}{π}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{{π}^{2}}$ |
| A. | $\sqrt{3}$-i | B. | $\sqrt{3}$+i | C. | -$\sqrt{3}$-i | D. | -$\sqrt{3}$+i |
| A. | ∅ | B. | M | C. | N | D. | {x|0<x<1} |
 运行如图所示的程序框图,则输出S的值为( )
运行如图所示的程序框图,则输出S的值为( )| A. | -3 | B. | -2 | C. | 4 | D. | 8 |