题目内容

15．若函数f（x）=（a-1）x3+ax2为奇函数，则f（1）=（　　）
A．1B．-1C．-2D．0

分析 利用奇函数的定义，求出a，再计算f（1）即可．

解答 解：∵f（x）=（a-1）x3+ax2为奇函数，
∴-（a-1）x3+ax2=-（a-1）x3-ax2，
∴a=0，
∴f（x）=-x3，∴f（1）=-1，
故选B．

点评 本题考查奇函数的定义，考查学生的计算能力，比较基础．

练习册系列答案
相关题目
16．先把函数y=sin（x+φ）的图象上个点的横坐标缩短为原来的$\frac{1}{2}$（纵坐标不变），再向右平移$\frac{π}{3}$个单位，所得函数关于y轴对称，则φ的值可以是（　　）
A．$\frac{π}{6}$B．$\frac{π}{3}$C．$-\frac{π}{6}$D．$-\frac{π}{3}$
6．已知二次函数f（x）=-x2+ax+b（a，b∈R），设M（a，b）是函数g（x）=|f（x）|在[1，2]上的最大值．
（1）当a=1时，求M（1，b）关于b的解析式；
（2）若对任意的a，b∈R，恒有M（a，b）≥M（a0，b0），求满足条件的所有实数对（a0，b0）．
3．如图所示的程序框图，若f（x）=logax，g（x）=lnx，输入x=2016，则输出的h（x）=（　　）
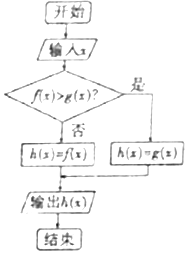
A．2016B．2017C．loga2016D．loga2017
10．已知函数f（x）=x2-2ax+4
（1）求函数y=f（x），x∈[0，2]的最小值
（2）若对任意x1，x2∈[0，2]，都有|f（x1）-f（x2）|＜4恒成立，求a的取值范围．
20．已知△ABC中，内角A，B，C的对边分别为a，b，c，且a，b，c成等差数列，C=2A．
（1）求cosA；
（2）设$a=\frac{{4{m^2}+4m+9}}{m+1}$（m＞0），求△ABC的面积的最小值．
7．已知函数f（x）=$\sqrt{{2}^{x}+\frac{a}{{2}^{x}}-2}$．
（1）若f（x）的定义域为R，求实数a的取值范围；
（2）若f（x）的值域为[0，+∞），求实数a的取值．
4．已知数列{an}满足an+1=an+$\frac{1}{2}$，则数列{an}是（　　）
A．递增数列B．递减数列C．摆动数列D．常数列
5．若函数f（x）=$\frac{kx+7}{{k{x^2}+4kx+3}}$的定义域为R，则实数k的取值范围是（　　）
A．$（{0，\frac{3}{4}}）$B．$（{-∞，0}）∪（{\frac{3}{4}，+∞}）$C．$[{0，\frac{3}{4}}）$D．$（{\frac{3}{4}，+∞}）$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网