题目内容
12．已知2sin2α=1+cos2α，则tan（α+$\frac{π}{4}$）的值为（ ）| A． | -3 | B． | 3 | C． | -3或3 | D． | -1或3 |
分析 由倍角公式求得sinα与cosα的数量关系，结合正弦、余弦以及正切函数的转化关系进行解答即可．
解答 解：∵2sin2α=1+cos2α，
∴4sinαcosα=1+2cos2α-1，
即2sinαcosα=cos2α，
①当cosα=0时，$α=kπ+\frac{π}{2}$，此时$tan（{α+\frac{π}{4}}）=-1$，
②当cosα≠0时，$tanα=\frac{1}{2}$，此时$tan（{α+\frac{π}{4}}）=\frac{{tanα+tan\frac{π}{4}}}{{1-tanαtan\frac{π}{4}}}=3$，
综上所述，tan（α+$\frac{π}{4}$）的值为-1或3．
故选：D．
点评 此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键，难度不大．
练习册系列答案
相关题目
如图所示的几何体是由正四棱锥和圆柱组合而成，且该几何体内接于球（正四棱锥的顶点都在球面上），正四棱锥底面边长为2，体积为$\frac{4}{3}$，则圆柱的体积为2π．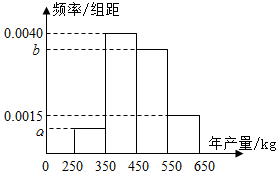
某人租用一块土地种植一种瓜类作物，租期5年，根据以往的年产量数据，得到年产量频率分布直方图如图所示，以各区间中点值作为该区间的年产量，得到平均年产量为455kg．当年产量低于450kg时，单位售价为12元/kg，当年产量不低于450kg时，单位售价为10元/kg．