题目内容
19.若非空集合A,B,C满足A∩B=C,且A不是B的子集,则“x∈C”是“x∈A”的( )| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
分析 由于A∩B=C,且A不是B的子集,由“x∈C”可得“x∈A”,反之不成立.即可判断出.
解答 解:A∩B=C,且A不是B的子集,
则“x∈C”⇒“x∈A”,反之不成立.
∴“x∈C”是“x∈A”的充分不必要条件.
故选:A.
点评 本题考查了元素与集合之间的关系、集合之间的关系、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
9.在空间中,已知$\overrightarrow{AB}$=(2,4,0),$\overrightarrow{BC}$=(-1,3,0),则∠ABC的大小为( )
| A. | 45° | B. | 90° | C. | 120° | D. | 135° |
14.已知实数x,y满足$\left\{\begin{array}{l}y-1≥0\\ 2x-y-1≥0\\ x+y-m≤0\end{array}\right.$,若x-y的最大值为6,则实数m=8.
8.已知梯形ABCD中,AD∥BC,∠ABC=90°,AD=2,BC=1,P是腰AB上的动点,则|$\overrightarrow{PC}$+$\overrightarrow{PD}$|的最小值为3.
9.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右顶点分别为A、B,虚轴的端点在以原点为圆心,|AB|为直径的圆上,P为该双曲线上一点,若直线PB的斜率为$\sqrt{2}$,则直线PA的斜率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
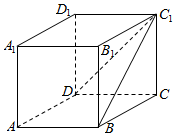 如图所示,直四棱柱ABCD-A1B1C1D1的底面是直角梯形,∠BAD=∠ADC=90°,过C1的平面交底面ABCD于BD,若AA1=2$\sqrt{2}$,AB=AD=2,CD=2AB,求:
如图所示,直四棱柱ABCD-A1B1C1D1的底面是直角梯形,∠BAD=∠ADC=90°,过C1的平面交底面ABCD于BD,若AA1=2$\sqrt{2}$,AB=AD=2,CD=2AB,求: