题目内容
设函数f(x)=
,若f(a)=4,则实数a= .
|
考点:函数的零点,函数的值
专题:函数的性质及应用
分析:利用分段函数的性质求解.
解答:
解:∵f(x)=
,f(a)=4,
∴当a≤0时,f(a)=2-a=4,解得a=-2,
当a>0时,f(a)=log2a=4,a=16.
故答案为:-2或16.
|
∴当a≤0时,f(a)=2-a=4,解得a=-2,
当a>0时,f(a)=log2a=4,a=16.
故答案为:-2或16.
点评:本题考查满足条件的实数值的求法,是基础题,解题时要注意函数性质的合理运用.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
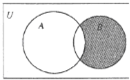 设区间U={1,2,3,4,5,6,7,8,9},集合A={1,2,3,5},B={2,4,6,7},则图中的阴影部分表示的集合为( )
设区间U={1,2,3,4,5,6,7,8,9},集合A={1,2,3,5},B={2,4,6,7},则图中的阴影部分表示的集合为( )| A、{2} |
| B、{4,6,7} |
| C、{1,2,5} |
| D、{4,6,7,8} |
设全集U=Z,集合M={1,2},P={-2,-1,0,1,2},则P∩∁UM=( )
| A、{0} | B、{1} |
| C、{-1,-2,0} | D、∅ |
已知集合A={x|x-2=0},B={0,1,2},则A∩B=( )
| A、{0} | B、{0,1,} |
| C、{2} | D、{0,1,2} |

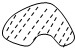 如图,边长为2的正方形中有一封闭曲线围成的阴影区域.在正方形中随机撒一粒豆子,它落在阴影区域内的概率为
如图,边长为2的正方形中有一封闭曲线围成的阴影区域.在正方形中随机撒一粒豆子,它落在阴影区域内的概率为