题目内容
已知:a=(2
)
-(9.6)0-(3
)-
+(1.5)-2,b=(log43+log83)(log32+log92)÷(log224+lg
-log3
+lg2-log23),求a+3b的值.
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 8 |
| 2 |
| 3 |
| 1 |
| 2 |
| 27 |
考点:对数的运算性质
专题:函数的性质及应用
分析:利用指数、对数的性质和换底公式求解.
解答:
解:∵a=(2
)
-(9.6)0-(3
)-
+(1.5)-2
=
-1-
+
=
,
b=(log43+log83)(log32+log92)÷(log224+lg
-log3
+lg2-log23)
=(log6427+log649)(log94+log92)÷(log28+lg1-
)
=
×
÷
=
×
=
.
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 8 |
| 2 |
| 3 |
=
| 3 |
| 2 |
| 4 |
| 9 |
| 4 |
| 9 |
=
| 1 |
| 2 |
b=(log43+log83)(log32+log92)÷(log224+lg
| 1 |
| 2 |
| 27 |
=(log6427+log649)(log94+log92)÷(log28+lg1-
| 3 |
| 2 |
=
| lg(27×9) |
| lg64 |
| lg8 |
| lg9 |
| 3 |
| 2 |
=
| 5 |
| 4 |
| 2 |
| 3 |
=
| 5 |
| 6 |
点评:本题考查代数和的求法,是基础题,解题时要注意指数、对数的性质和换底公式的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列函数中,值域为R的是( )
A、f(x)=
| ||
| B、f(x)=2x | ||
| C、f(x)=ln(x2+1) | ||
| D、f(x)=lg(x+1) |
| (lg9-1)2 |
| A、lg9-1 | ||
| B、1-lg9 | ||
| C、8 | ||
D、2
|
设全集U=Z,集合M={1,2},P={-2,-1,0,1,2},则P∩∁UM=( )
| A、{0} | B、{1} |
| C、{-1,-2,0} | D、∅ |
 如图,边长为2的正方形中有一封闭曲线围成的阴影区域.在正方形中随机撒一粒豆子,它落在阴影区域内的概率为
如图,边长为2的正方形中有一封闭曲线围成的阴影区域.在正方形中随机撒一粒豆子,它落在阴影区域内的概率为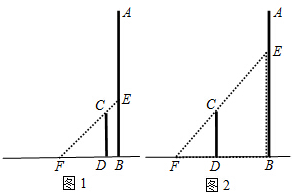 如图所示,直立在地面上的两根钢管AB和CD,AB=10
如图所示,直立在地面上的两根钢管AB和CD,AB=10