题目内容
7．下列函数中，导函数是奇函数的是（ ）| A． | y=cosx | B． | y=ex | C． | y=lnx | D． | y=ax |
分析 运用常见函数导数的公式和奇偶性的定义，即可判断A正确．
解答 解：A，y=cosx的导数为y′=-sinx，显然为奇函数；
B，y=ex的导数为y′=ex为非奇非偶函数；
C，y=lnx的导数为y′=$\frac{1}{x}$（x＞0）为非奇非偶函数；
D，y=ax的导数为y′=axlna为非奇非偶函数．
故选：A．
点评 本题考查函数的奇偶性的判断和函数的导数公式的运用，考查判断能力，属于基础题．
练习册系列答案
名校名师培优作业本加核心试卷系列答案
全程金卷系列答案
相关题目
15．
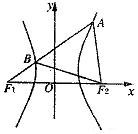如图，F1，F2分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的左、右焦点，过F1的直线l与双曲线分别交于点A，B，若△ABF2为等边三角形，则双曲线的渐近线的斜率为（ ）
如图，F1，F2分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的左、右焦点，过F1的直线l与双曲线分别交于点A，B，若△ABF2为等边三角形，则双曲线的渐近线的斜率为（ ）| A． | ±$\sqrt{3}$ | B． | ±2 | C． | $±\sqrt{6}$ | D． | ±$\sqrt{2}$ |
16．若扇形的圆心角为$\frac{2}{3}$π弧度，r=2，则扇形的面积是（ ）
| A． | $\frac{8}{3}$π | B． | $\frac{4}{3}$ | C． | $\frac{3}{2}π$ | D． | $\frac{4}{3}$π |