题目内容
若正多边形有n条边，它们对应的向量依次为
，
，…，
，则这n个向量（ ）
| a1 |
| a2 |
| an |
| A、都相等 | B、都共线 |
| C、都不共线 | D、模都相等 |
考点：向量的模
专题：平面向量及应用
分析：利用正多边形的定义可知：这n个向量的模都相等．
解答：
解：正多边形有n条边，它们对应的向量依次为
，
，…，
，
则|
|=|
|=…=|
|．
故选：D．
| a1 |
| a2 |
| an |
则|
| a1 |
| a2 |
| an |
故选：D．
点评：本题考查了正多边形的定义、向量的模，属于基础题．
练习册系列答案
相关题目
点F（c，0）为双曲线
-
=1（a＞0，b＞0）的右焦点，点P在双曲线上，线段PF与圆（x-
）2+y2=
相切于点Q，且
=2
，则双曲线的离心率等于（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| c |
| 3 |
| b2 |
| 9 |
| PQ |
| QF |
A、
| ||
B、
| ||
C、
| ||
| D、2 |
圆x2+y2+2kx+k2-1=0与圆x2+y2+2（k+1）y+k2+2k=0的圆心之间的最短距离是（ ）
A、
| ||||
B、2
| ||||
| C、1 | ||||
D、
|
函数y=
在[0，2]上的最大值（ ）
| x |
| ex |
| A、当x=0时，y=0 | ||||||
B、当x=2时，y=
| ||||||
C、当x=1时，y=
| ||||||
D、当x=
|
若sin2θ-1+（
+1）i是纯虚数，则θ的值为（ ）
| 2 |
A、2kπ-
| ||||
B、kπ+
| ||||
C、2kπ±
| ||||
D、
|
在△ABC中，已知b=40，c=20，C=60°，则此三角形的解的情况是（ ）
| A、有一解 | B、有两解 |
| C、无解 | D、有解但解的个数不确定 |
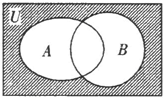设全集U={1，2，3，4，5，6，7，8}，集合A={2，4，5，7}，B={1，4，7，8}，那么如图所示的阴影部分所表示的集合是（ ）| A、{3，6} |
| B、{4，7} |
| C、{1，2，4，5，7，8} |
| D、{1，2，3，5，6，8} |
根据如图给出的数塔猜测123456×9+7=（ ）
| A、1111110 |
| B、1111111 |
| C、1111112 |
| D、1111113 |