题目内容
 如图所示,已知在四面体ABCD中,AB⊥BD,△ABC与△BCD是两个全等的等腰直角三角形,AB=BC=CD.
如图所示,已知在四面体ABCD中,AB⊥BD,△ABC与△BCD是两个全等的等腰直角三角形,AB=BC=CD.(1)求证:平面ABC⊥平面ACD;
(2)求直线AD与平面ABC所成的角的余弦值.
考点:平面与平面垂直的判定,直线与平面所成的角
专题:空间位置关系与距离
分析:(1)由△ABC是等腰直角三角形,推导出AB⊥CD,由△BCD是等腰直角三角形,推导出CD⊥BC,由此能证明面ABC⊥面ACD.
(2)由CD⊥面ABC,推导出∠DAC为直线AD与平面ABC所成的角,由此能求出直线AD与平面ABC所成角的余弦值.
(2)由CD⊥面ABC,推导出∠DAC为直线AD与平面ABC所成的角,由此能求出直线AD与平面ABC所成角的余弦值.
解答:
 证明:(1)∵△ABC是等腰直角三角形,AB=BC,
证明:(1)∵△ABC是等腰直角三角形,AB=BC,
∴AB⊥BC …(1分)
又∵AB⊥BD BC∩BD=B,BC?面BCD,BD?面BCD,…(2分)
∴AB⊥面BCD …(3分)
又∵CD?面BCD
∴AB⊥CD…(4分)
又∵△BCD是等腰直角三角形,BC=CD,
∴CD⊥BC,…(5分)
又∵AB∩BC=B,AB?面ABC,BC?面ABC,
∴CD⊥面ABC,…(7分)
又∵CD?面ACD,
∴面ABC⊥面ACD.…(8分)
(2)∵CD⊥面ABC,
∴AC为直线AD在平面ABC内的射影,
∴∠DAC为直线AD与平面ABC所成的角,…(10分)
设AB=BC=CD=a,则AC=BD=
a,AD=
a,
∴在Rt△ACD中,cos∠DAC=
=
.…(11分)
∴直线AD与平面ABC所成角的余弦值为
.…(12分)
 证明:(1)∵△ABC是等腰直角三角形,AB=BC,
证明:(1)∵△ABC是等腰直角三角形,AB=BC,∴AB⊥BC …(1分)
又∵AB⊥BD BC∩BD=B,BC?面BCD,BD?面BCD,…(2分)
∴AB⊥面BCD …(3分)
又∵CD?面BCD
∴AB⊥CD…(4分)
又∵△BCD是等腰直角三角形,BC=CD,
∴CD⊥BC,…(5分)
又∵AB∩BC=B,AB?面ABC,BC?面ABC,
∴CD⊥面ABC,…(7分)
又∵CD?面ACD,
∴面ABC⊥面ACD.…(8分)
(2)∵CD⊥面ABC,
∴AC为直线AD在平面ABC内的射影,
∴∠DAC为直线AD与平面ABC所成的角,…(10分)
设AB=BC=CD=a,则AC=BD=
| 2 |
| 3 |
∴在Rt△ACD中,cos∠DAC=
| AC |
| AD |
| ||
| 3 |
∴直线AD与平面ABC所成角的余弦值为
| ||
| 3 |
点评:本题考查平面与平面垂直的证明,考查直线与平面所成角的余弦值的求法,解题时要注意空间思维能力的培养.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知角α的终边经过点(12,-5),则sinα等于( )
A、
| ||
B、-
| ||
C、
| ||
D、-
|
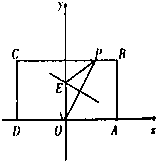 如图,在矩形ABCD中,已知A(2,0),C(-2,2),点P在BC边上移动,线段OP的垂直平分线交y轴于点E,点M满足
如图,在矩形ABCD中,已知A(2,0),C(-2,2),点P在BC边上移动,线段OP的垂直平分线交y轴于点E,点M满足 如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D,E分别在棱PB,PC上,且DE∥BC.
如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D,E分别在棱PB,PC上,且DE∥BC.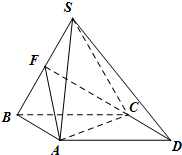 四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠DAB=135°,BC=2
四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠DAB=135°,BC=2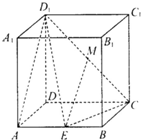 在长方体ABCD-A1B1C1D1中,AD=1,AA1=AB=2.点E是线段AB上的动点,点M为D1C的中点.
在长方体ABCD-A1B1C1D1中,AD=1,AA1=AB=2.点E是线段AB上的动点,点M为D1C的中点.