题目内容
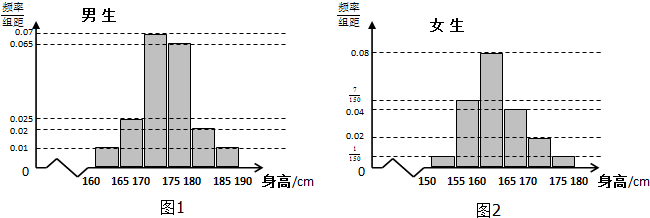
在正方体ABCD-A1B1C1D1中，BD1与AC所成的角是（ ）
| A、60° | B、30° |
| C、90° | D、45° |
考点：异面直线及其所成的角
专题：空间角
分析：由已知得AC⊥BD，AC⊥DD1，从而AC⊥平面DBB1D1，由此能求出BD1与AC所成的角的大小．
解答：
解：在正方体ABCD-A1B1C1D1中，
∵ABCD是正方形，∴AC⊥BD，
∵DD1⊥平面ABCD，∴AC⊥DD1，
∵BD∩DD1=D，
∴AC⊥平面DBB1D1，
∵BD1?平面DBB1D1，
∴AC⊥BD1，
∴BD1与AC所成的角是90°．
故选：C．
解：在正方体ABCD-A1B1C1D1中，∵ABCD是正方形，∴AC⊥BD，
∵DD1⊥平面ABCD，∴AC⊥DD1，
∵BD∩DD1=D，
∴AC⊥平面DBB1D1，
∵BD1?平面DBB1D1，
∴AC⊥BD1，
∴BD1与AC所成的角是90°．
故选：C．
点评：本题考查异面直线所成角的大小的求法，是基础题，解题时要注意空间思维能力的培养．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
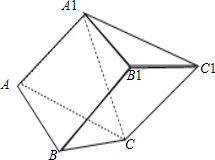已知斜三棱柱ABC-A1B1C1 的侧面 A1ACC1与底面ABC垂直，∠ABC=90°，BC=2，AC=2